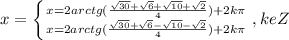Я не уверен, что это правильно
2)
Упростить уравнение,используя универсальную тригонометрическую подстановку:
;
Решить уравнение относительно t:
Сделать обратную подстановку t=tg():
)=\frac{\sqrt{30}+\sqrt{6}+\sqrt{10}+\sqrt{2}}{4}\\
tg(\frac{x}{2} )=\frac{\sqrt{30}+\sqrt{6}-\sqrt{10}-\sqrt{2}}{4} [/tex];
Решить уравнение относительно x:
x=2arctg()+2kπ,k∈Z
x=2arctg()+2kπ,k∈Z;
Поскольку универсальная замена переменной может быть использована только если x≠π+2kπ,k∈Z,то необходимо проверить является ли x=π+2kπ,k∈Z также решением уравнения:
Упростить выражение,используя cos(+-2*k*π)=cos(t),k∈Z:
Упростить равенство:
1,23607=0;
π+2kπ,k∈Z не является решением,следовательно,его не нужно добавлять:
ответ:
Я не уверен, что это правильно
2)
Упростить уравнение,используя универсальную тригонометрическую подстановку:
Решить уравнение относительно t:
Сделать обратную подстановку t=tg(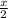 ):
):
tg(\frac{x}{2} )=\frac{\sqrt{30}+\sqrt{6}-\sqrt{10}-\sqrt{2}}{4} [/tex];
Решить уравнение относительно x:
x=2arctg(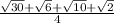 )+2kπ,k∈Z
)+2kπ,k∈Z
x=2arctg(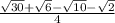 )+2kπ,k∈Z;
)+2kπ,k∈Z;
Поскольку универсальная замена переменной может быть использована только если x≠π+2kπ,k∈Z,то необходимо проверить является ли x=π+2kπ,k∈Z также решением уравнения:
Упростить выражение,используя cos(+-2*k*π)=cos(t),k∈Z:
Упростить равенство:
1,23607=0;
π+2kπ,k∈Z не является решением,следовательно,его не нужно добавлять:
x=2arctg(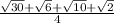 )+2kπ,k∈Z
)+2kπ,k∈Z
x=2arctg(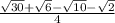 )+2kπ,k∈Z;
)+2kπ,k∈Z;
ответ: