1. 1) Дробь называется неправильной, если числитель больше или равен знаменателю, у ВАС, когда a ≤ 20, должно выполняться неравенство 20/а <2; 10/а<1;⇒a > 10, т.е. а∈(10;20], найдем теперь множество натуральных, попадающих в данный промежуток.
a = {11;12;13;14;15;16;17;18;19;20}
2) когда a ≤ 4, должно выполняться неравенство 4/а >а; решим неравенство методом интервалов.4/а-а>0; (4-а²)/а>0, это неравенство равносильно такому а(2-а)(2+а) >0
-202
+ - + -
Решением этого неравенства служат а∈(-∞;-2)∪(0;2), учитав, что а- натуральное, a ≤ 4, получаем, что таким а является только одно число а=1.
1. 1) Дробь называется неправильной, если числитель больше или равен знаменателю, у ВАС, когда a ≤ 20, должно выполняться неравенство 20/а <2; 10/а<1;⇒a > 10, т.е. а∈(10;20], найдем теперь множество натуральных, попадающих в данный промежуток.
a = {11;12;13;14;15;16;17;18;19;20}
2) когда a ≤ 4, должно выполняться неравенство 4/а >а; решим неравенство методом интервалов.4/а-а>0; (4-а²)/а>0, это неравенство равносильно такому а(2-а)(2+а) >0
-202
+ - + -
Решением этого неравенства служат а∈(-∞;-2)∪(0;2), учитав, что а- натуральное, a ≤ 4, получаем, что таким а является только одно число а=1.
2. Раздробим единицу как 40/40, 1 - 13/40 = 40/40 - 13/40 = 27/40
3. n < 123/30 = 4 3/30 =>n < 123/30 = 4.1; n = 4 - наибольшее натуральное n, удовлетворяющее данному неравенству.
4. 9 5/9-(х+3 7/9)=5 4/9
9 5/9 - 5 4/9=x + 3 7/9
x + 3 7/9 = 4 1/9
x = 4 1/9 - 3 7/9
x = 37/9 - 34/9
x = 3/9
x = 1/3
Для того чтобы высчитать площадь фигуры неразрывной функции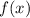
на некотором промежутке, следует воспользоваться формулой Ньютона — Лейбница:
Здесь
и 
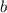— границы фигуры на оси абсцисс, 
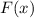— первообразная для функции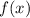 
2) Здесь имеем площадь фигуры, ограниченной двумя функциям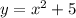и:
и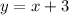 
.
Чтобы найти данную площадь, нужно найти разность площадей каждой функции.
Очевидно, что площадь фигуры, образованной функцией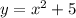
на отрезке ![[-2; \ 1]](/tpl/images/1068/9083/4704b.png)
больше, чем площадь фигуры, образованной функцией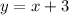 
на том же отрезке, поэтому