1. Боковые грани призмы являются …
2. Высота прямой призмы равна её …
3. Все высоты призмы …
4. Прямоугольный параллелепипед, у которого все три измерения равны, есть …
5. Перпендикуляр, проведенный из какой-нибудь точки одного основания призмы к
плоскости другого, есть …
6. Если боковые ребра призмы перпендикулярны к основаниям, то призма …
7. Если боковые ребра призмы не перпендикулярны к основаниям, то призма ….
8. Если в основании прямой призмы лежит правильный многоугольник, то призма …
9. Основания призмы лежат в плоскостях, которые являются …
10. Отрезок, соединяющий две вершины, не принадлежащие одной грани, есть …

Пошаговое объяснение:

1) 1 из 10 представляет собой десятую часть, значит, нужно разделить 10 на равные между собой части, и тогда мы найдём 1 из 10.

10/10 = 1

2) Произведение - это результат умножения.

, где a - первый множитель, b - второй множитель, c - произведение.

Чтобы найти один из множителей, надо произведение поделить на другой множитель.

Пример: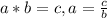

3)Частное - это результат деления.

, где a - делимое (потому что это число делят), b -  делитель ( потому что на это число делят), c - частное.

Чтобы найти делимое, нужно частное умножить на делитель.

a = c*b (Пример: 10/2 = 5, 10 = 5 * 2)

4) Чтобы найти делитель, нужно делимое разделить на частное

b = a/c (Пример: 10/2 = 5, 2 = 10/5)

Верные утверждения:

1) Теорема: параллелограмм является прямоугольником, если: а) его диагонали равны; б) серединный перпендикуляр к какой-либо стороне параллелограмма является его осью симметрии.

2) Квадрат - это прямоугольник, у которого все стороны являются равными.

6) Сумма внутренних углов параллелограмма = 360°.

7) Они могут быть равны, если это ромб. Но во всех остальных случаях это так.

10) Жесткая фигура — это фигура, не подверженная деформации.

Неверные утверждения:

3) Квадрат, прямоугольник и ромб - это частные случаи параллелограмма. Не все и не всегда.

4) Квадрат, прямоугольник и ромб - это частные случаи параллелограмма. Значит, такое возможно.

5) Квадрат обладает всеми свойствами ромба, параллелограмма и прямоугольника. Квадрат - это всегда параллелограмм.

8) Теорема: диагонали параллелограмма делятся точкой пересечения пополам.

9) Такое возможно не всегда, а только в одном случае, когда параллелограмм - ромб.