1. Цена на товар в середине года подорожала на 40 %. В конце года цена товара снизилась еще на 20 96, и товар был продан за 4200 тенге, Определи начальную цену товара. у меня сор лаю 15б
Так как угол ADC равен π/3, то есть 60°, и DE - биссектриса угла ADC, то углы ADE и CDE равны по 60°:2=30°.
Сумма смежных углов параллелограмма равна 180°, значит:
∠BCD=180°-∠ADC=180°-60°=120°
Так как угол BCD равен 120° и CE - биссектриса угла BCD, то углы BCE и DCE равны по 120°:2=60°.
Рассмотрим треугольник CDE. Так как два угла в нем известны, то найдем третий угол CED:
∠CED=180°-∠CDE-∠DCE=180°-30°-60°=90°
Значит, треугольник CDE - прямоугольный.
В прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы.
Введем обозначения. Пусть катет CE, лежащий против угла в 30°, равен a. Тогда гипотенуза CD равна 2а. Заметим, что CD соответствует одной из сторон параллелограмма.
Рассмотрим треугольник ВСЕ. Найдем неизвестные его углы.
Так как противоположные углы параллелограмма равны, то:
∠ABC=∠ADC=60°
Зная два угла треугольника, найдем третий:
∠BEC=180°-∠BCE-∠CBE=180°-60°-60°=60°
Все углы треугольника ВСЕ равны, значит он - равносторонний.
Одна из сторон треугольника ВСЕ обозначена как а, значит и все его стороны равны а. В том числе, сторона параллелограмма ВС=а.
Таким образом, известны в наших обозначениях стороны параллелограмма: AB=DC=2a, BC=AD=a.
Рассмотрим треугольник АВС. Запишем для него теорему косинусов:
Подставим известные соотношения:
По условию АС=3.
(отрицательный корень смысла не имеет)
Вернемся к треугольнику CDE. Две стороны в нем теперь известны: , . Запишем теорему Пифагора:
Так как угол ADC равен π/3, то есть 60°, и DE - биссектриса угла ADC, то углы ADE и CDE равны по 60°:2=30°.
Сумма смежных углов параллелограмма равна 180°, значит:
∠BCD=180°-∠ADC=180°-60°=120°
Так как угол BCD равен 120° и CE - биссектриса угла BCD, то углы BCE и DCE равны по 120°:2=60°.
Рассмотрим треугольник CDE. Так как два угла в нем известны, то найдем третий угол CED:
∠CED=180°-∠CDE-∠DCE=180°-30°-60°=90°
Значит, треугольник CDE - прямоугольный.
В прямоугольном треугольнике катет лежащий против угла в 30° равен половине гипотенузы.
Введем обозначения. Пусть катет CE, лежащий против угла в 30°, равен a. Тогда гипотенуза CD равна 2а. Заметим, что CD соответствует одной из сторон параллелограмма.
Рассмотрим треугольник ВСЕ. Найдем неизвестные его углы.
Так как противоположные углы параллелограмма равны, то:
∠ABC=∠ADC=60°
Зная два угла треугольника, найдем третий:
∠BEC=180°-∠BCE-∠CBE=180°-60°-60°=60°
Все углы треугольника ВСЕ равны, значит он - равносторонний.
Одна из сторон треугольника ВСЕ обозначена как а, значит и все его стороны равны а. В том числе, сторона параллелограмма ВС=а.
Таким образом, известны в наших обозначениях стороны параллелограмма: AB=DC=2a, BC=AD=a.
Рассмотрим треугольник АВС. Запишем для него теорему косинусов:
Подставим известные соотношения:
По условию АС=3.
Вернемся к треугольнику CDE. Две стороны в нем теперь известны: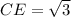
, 
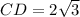. Запишем теорему Пифагора:
Выражаем искомый отрезок DE:
ответ: 3
а) 1/12 и 1/35 = 35/420 и 12/420
12=2*2*3 35=5*7 НОК (12 и 35) = 12 * 35 = 420
420 : 12 = 35 - доп.множ. к 1/12 = (1*35)/(12*35) = 35/420
420 : 35 = 12 - доп.множ. к 1/35 = (1*12)(35*12) = 12/420
б) 17/96 и 41/72 = 51/288 и 164/288
96=2*2*2*2*2*3 72=2*2*2*3*3 НОК(96и72)=2*2*2*2*2*3*3=288
288 : 96 = 3 - доп.множ. к 17/96 = (17*3)/(96*3) = 51/288
288 : 72 = 4 - доп.множ. к 41/72 = (41*4)/(72*4) = 164/288
в) 5/56 и 17/29 = 145/1624 и 952/1624
56*29=1624 - наименьший общий знаменатель число)
1624 : 56 = 29 - доп.множ. к 5/56 = (5*29)/(56*29) = 145/1624
1624 : 29 = 56 - доп.множ. к 17/29 = (17*56)/(29*56) = 952/1624
г) 5/17 и 9/13 = 65/221 и 153/221
17*13=221-наименьший общий знаменатель (17и числа)
221 : 17 = 13 - доп.множ. к 5/17 = (5*13)/(17*13) = 65/221
221 : 13 = 17 - доп.множ. к 9/13 = (9*17)/(13*17) = 153/221
там ещё ест другие дроби