1. Дано множество: B = {xe N| 80 < x < 100 H x 9}. а) Истинно или Ложно? Натуральное число кратно 9 тогда и только тогда, когда его последняя цифра делится на 9“. б) Задайте множество В перечисле- нием его элементов. В) Выберите одно четное число и одно нечетное число среди элемен- тов множества Ви найдите их HOK. 2. Дана и ее бабушка вместе собрали 106 кг огурцов. Огурцы распреде- лили по 14 кг в каждый из ящиков, имеющихся у бабушки, и осталось еще 8 кг. а) Впишите натуральное число: 13 = 8. = 8 б) Определите, сколько ящиков было у бабушки. в) Найдите сумму денег, которую получит бабушка после продажи всех ящиков с огурцами по цене 7 леев/кг. 3. Решите на множестве N уравнение: 2* 3* - 5x = 21.
ИССЛЕДОВАНИЕ 1. Область определения. Деление на ноль в знаменателе. Х≠ 1. Х∈(-∞;0)∪(0;+∞) 2. Вертикальная асимптота: Х= 1. 3. Пересечение с осью Х. Y(x) = 0 - нет. 4. Пересечение с осью У - нет 5. Наклонная асимптота k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность. Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x) Функция ни четная ни нечетная. 7. Поведение в точке разрыва. lim(->0-) Y(x) = -∞. lim(->0+) Y(x) = +∞ 8, Первая производная. 6. Локальные экстремумы. Y'(x) = 0, x1 = - 3/2, x2 = 3/2 Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12. 7. Участки монотонности функции. Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2] 8. Вторая производная.
Корней нет. Точек перегиба (на графике) - нет. 9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
Жили были очень добрые куклы они решили построить кому нибудь домик. А в это время ежик жираф и крокодил потеряли домик из-за злого медведя . Они очень грустили и решили начать строить новый дом . К ним пришли на куклы . Ежик хотел себе уютный красивый домик , жираф хотел большой просторный дом , а крокодил хотел дом с бассеином, Они очень много спорили какой дом лучше построить . Потом пришли куклы и сказали что это все можно совместить все их желания . Они начали работу трудились 3 месяца . Наступила осень они достроили свой домик и вышли посмотреть на него у них получился целый катедж . Они поблагодорили кукл и жили в своем диме долго и счастливо . Вот и сказки конец а кто слушал молодец
ДАНО
Y = (x² + 9)/x
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность.
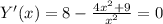
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.
Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
10. График в приложении