1.Даны два числовых множества М=(5;15) и К=[-3;10]. Изобразить и выполнить М∩К, МUК, М\К, К\М 1.Даны два числовых множества М=(0;10) и К=[-2;8].

Изобразить и выполнить М∩К, МUК, М\К,К\М

2. Даны множества

М=[-2;6], Q=(3;7), S=[0;5]. Изобразить и выполнить множество МUQ\S 2. Даны множества

М=[-1;7], Q=[-6;6], S=[-2;8]. Изобразить и выполнить множество М∩S\Q

​

Всего израсходовали 7.28 ц или 728 кг цемента (7.28*100 = 728)

3-й день: х (кг) цемента

2-й день: 2х (кг) цемента

1-й день: 2*2x (кг) цемента

Составляем и решаем уравнение:

    x+2x+4x = 728

    7x = 728

    x = 104

Находим, сколько килограммов цемента расходовали каждый день:

x = 104 кг — цемента израсходовали в 3-й день2х = 2*104 = 208 кг — цемента израсходовали во 2-й день2*2x = 2*2*104 = 4*104 = 416 кг — цемента израсходовали в 1-й день

ответ: В первый, второй и третий день израсходовали 416, 208 и 104 кг цемента соответствено.

Пусть катет треугольника равен а. Тогда гипотенуза равна .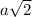

Есть два составлять квадрат.

1. Составим из двух таких треугольников квадратик (треугольники совместим по гипотенузе). Так как треугольников дано 50, то квадратиков мы можем получить вдвое меньше, то есть 25. Уже из таких квадратиков (сторона которых равна а) будем составлять разные квадраты.

Первый квадрат - это один такой квадратик (сторона а)

Далее, квадрат из 4 квадратиков (сторона 2а)

Квадрат из 9 квадратиков (сторона 3а)

Квадрат из 16 квадратиков (сторона 4а)

Квадрат из 25 квадратиков (сторона 5а)

Больше 25 квадратиков мы использовать не можем.

Итого, у нас получилось 5 различных квадратов.

2. Составим из четырех таких треугольников квадратик (треугольники совместим по катетам). Так как треугольников дано 50, то таких квадратиков можем получить в четыре раза меньше, то есть 12 (еще два треугольника останутся незадействованными). Из таких квадратиков (сторона которых равна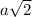 как гипотенуза исходного треугольника) будем составлять разные квадраты.

Один отдельно взятый квадратик (сторона )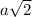

Квадрат из 4 квадратиков (сторона )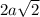

Квадрат из 9 квадратиков (сторона )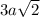

Квадрат из 16 и более квадратиков мы получить не можем, так как у нас есть только 12 квадратиков.

В этом случае, у нас получилось 3 различных квадрата, причем среди них нет квадратов, полученных в первой части решения.

Итого, 5+3=8 различных квадратов.

ответ: Г