Найдем общее число паролей без каких-либо дополнительных ограничений. Тогда, любая цифра может стоять на любом месте. Цифр для выбора 10, позиций в пароле 4, получаем:
вариантов
1. Рассмотрим первое ограничение: в паролей не может быть трех или четырех одинаковых цифр.
1.1. Найдем число паролей с тремя одинаковыми цифрами. Повторяющуюся цифру мы можем выбрать , оставшуюся уникальную цифру мы модем выбрать , кроме того есть разместить в пароле эту уникальную цифру. Получаем:
вариантов
1.2. Найдем число паролей с четырьмя одинаковыми цифрами. Интуитивно понятно, что имеется:
вариантов
2. Рассмотрим второе ограничение: в пароле не должно быть одновременно цифры 9 и двух цифр 1.
Начнем составлять заведомо неверный пароль. Включаем в него цифры 1, 1, 9 и некоторую цифру Х.
2.0. В качестве Х мы не рассматриваем цифру 1, так как сейчас мы уже рассматриваем пароли, удовлетворяющие первому условию, то есть трех одинаковых цифр в пароле быть не может.
2.1. В качестве цифры Х может быть цифра 9. Тогда, имеется две пары одинаковых цифр. Как-либо упорядочить их в пароле можно (ААВВ, АВАВ, АВВА, ВААВ, ВАВА, ВВАА). В этом случае имеется:
вариантов
2.2. В качестве цифры Х может быть цифра, отличная от 1 и 9. В этом случае у нас есть в 2 раза больше упорядочить эти цифры в пароле, показать эти размещения можно заменив в предыдущем перечислении цифры (В, В) сначала на цифры (C, D), а затем на цифры (D, C). Учитывая, что в качестве цифры Х может быть выбрана одна из 8 цифр, получим:
вариантов
3. Для определения числа правильных паролей из общего числа паролей вычтем все ограничения:
Відповідь:
Покрокове пояснення:
f(x)=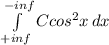 =1
=1
C∫_(-pi/2)^(pi/2) cos²xdx=C∫_(-pi/2)^(pi/2) (cos2x+1)/2 dx=
C/2 ∫_(-pi/2)^(pi/2) (cos2x+1)dx=C(1/4 sin2x+x/2) ║_(-pi/2)^(pi/2) =C(1/4*0+pi/4-0+pi/4)=C*pi/2=1 →C=2/pi
F(y)=2/pi \int\limits^{-inf}_{y} {cos^{2}x } \, dx=2/pi (1/4 sin2y+y/2)
M(x)=∫^{-inf}_{+inf}xf(x)dx=2/pi ∫_(-pi/2)^(pi/2) xcos²xdx=2/pi ∫_(-pi/2)^(pi/2) x(cos2x+1)/2 dx =1/pi ∫_(-pi/2)^(pi/2) (xcos2x+x) dx=
1/pi*(x²/2-x/2 sin2x+1/4 cos2x)║_(-pi/2)^(pi/2)=1/pi*0=0
D(x)=∫^{-inf}_{+inf} x²f(x)dx-(M(x))²=2/pi ∫_(-pi/2)^(pi/2) x²cos²xdx=
2/pi ∫_(-pi/2)^(pi/2) x²(cos2x+1)/2 dx=1/pi ∫_(-pi/2)^(pi/2) (x²cos2x+x²) dx=
1/pi*(x²/2*sin2x+x/2*cos2x-(sin2x)/4+x³/3)║_(-pi/2)^(pi/2)=1/pi*(pi/4*(-1)+pi/4*(-1)+pi³/12)=pi²/12-1/2=0,3225
стандартное отклонение
√D=√0,3225=0.56789
Пароль - последовательность четырех цифр.
Найдем общее число паролей без каких-либо дополнительных ограничений. Тогда, любая цифра может стоять на любом месте. Цифр для выбора 10, позиций в пароле 4, получаем:
1. Рассмотрим первое ограничение: в паролей не может быть трех или четырех одинаковых цифр.
1.1. Найдем число паролей с тремя одинаковыми цифрами. Повторяющуюся цифру мы можем выбрать , оставшуюся уникальную цифру мы модем выбрать , кроме того есть разместить в пароле эту уникальную цифру. Получаем:
1.2. Найдем число паролей с четырьмя одинаковыми цифрами. Интуитивно понятно, что имеется:
2. Рассмотрим второе ограничение: в пароле не должно быть одновременно цифры 9 и двух цифр 1.
Начнем составлять заведомо неверный пароль. Включаем в него цифры 1, 1, 9 и некоторую цифру Х.
2.0. В качестве Х мы не рассматриваем цифру 1, так как сейчас мы уже рассматриваем пароли, удовлетворяющие первому условию, то есть трех одинаковых цифр в пароле быть не может.
2.1. В качестве цифры Х может быть цифра 9. Тогда, имеется две пары одинаковых цифр. Как-либо упорядочить их в пароле можно (ААВВ, АВАВ, АВВА, ВААВ, ВАВА, ВВАА). В этом случае имеется:
2.2. В качестве цифры Х может быть цифра, отличная от 1 и 9. В этом случае у нас есть в 2 раза больше упорядочить эти цифры в пароле, показать эти размещения можно заменив в предыдущем перечислении цифры (В, В) сначала на цифры (C, D), а затем на цифры (D, C). Учитывая, что в качестве цифры Х может быть выбрана одна из 8 цифр, получим:
3. Для определения числа правильных паролей из общего числа паролей вычтем все ограничения:
ответ: 9528 паролей