1. Треугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками.
Приемлемо, однако следует добавить, что эти три точки не лежат на одной прямой.
2. Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести любую биссектрису, она будет являться медианой и высотой.
Это неверно. И медианой, и высотой является только биссектрисса угла, противолежащего основанию, а не любая.
3. Площадь любого треугольника можно вычислить по формулам:
и .
Верно.
4. Если в треугольник вписана окружность, то его площадь можно найти по формуле , где радиус этой окружности вычисляется по теореме косинусов: .
Неверно. Речь идет про описанную окружность, а не вписаную.
5. А если около треугольника описать окружность, то для нахождения площади треугольника справедлива формула
Здесь так же перепутаны вписанная и описанная окружности. Речь идет про вписанную окружности. К тому же ее радиус вычисляется по теореме синусов, а не косинусов.
6. Прямая, параллельная стороне треугольника, является его средней линией.
Неверно. Не всякая прямая, паралельная стороне треугольника является его средней линией. Можно дополнить тем, что прямая проходит через середину другой стороны, тогда это будет средняя линия.
7. Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники равны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники подобны.
В тексте приведен признак подобия треугольников, но не равенства. Не все прямоугольные треугольники подобны. Для подобия двух прямоугольных треугольников достаточно чтобы были равны два острых угла.
Исправленный вариант
Треугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками, не лежащими на одной прямой.
Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести биссектрису угла, противолежащего основанию, она будет являться медианой и высотой.
Площадь любого треугольника можно вычислить по формулам:
и .
Если около треугольника описана окружность, то его площадь можно найти по формуле , где радиус этой окружности вычисляется по теореме синусов:
А если в треугольник вписать окружность, то для нахождения площади треугольника справедлива формула .
Прямая, параллельная стороне треугольника и проходящая через его середину, является его средней линией.
Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники подобны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники с парой равных острых углов подобны.
1. Треугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками.
Приемлемо, однако следует добавить, что эти три точки не лежат на одной прямой.
2. Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести любую биссектрису, она будет являться медианой и высотой.
Это неверно. И медианой, и высотой является только биссектрисса угла, противолежащего основанию, а не любая.
3. Площадь любого треугольника можно вычислить по формулам:
Верно.
4. Если в треугольник вписана окружность, то его площадь можно найти по формуле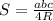 , где радиус этой окружности вычисляется по теореме косинусов:
, где радиус этой окружности вычисляется по теореме косинусов: 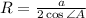 .
.
Неверно. Речь идет про описанную окружность, а не вписаную.
5. А если около треугольника описать окружность, то для нахождения площади треугольника справедлива формула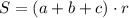
Здесь так же перепутаны вписанная и описанная окружности. Речь идет про вписанную окружности. К тому же ее радиус вычисляется по теореме синусов, а не косинусов.
6. Прямая, параллельная стороне треугольника, является его средней линией.
Неверно. Не всякая прямая, паралельная стороне треугольника является его средней линией. Можно дополнить тем, что прямая проходит через середину другой стороны, тогда это будет средняя линия.
7. Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники равны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники подобны.
В тексте приведен признак подобия треугольников, но не равенства. Не все прямоугольные треугольники подобны. Для подобия двух прямоугольных треугольников достаточно чтобы были равны два острых угла.
Исправленный вариантТреугольник – это геометрическая фигура, состоящая из трех точек, соединенных попарно отрезками, не лежащими на одной прямой.
Среди треугольников особенно выделяется равнобедренный треугольник. Если в нем провести биссектрису угла, противолежащего основанию, она будет являться медианой и высотой.
Площадь любого треугольника можно вычислить по формулам:
Если около треугольника описана окружность, то его площадь можно найти по формуле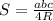 , где радиус этой окружности вычисляется по теореме синусов:
, где радиус этой окружности вычисляется по теореме синусов: 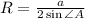
А если в треугольник вписать окружность, то для нахождения площади треугольника справедлива формула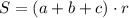 .
.
Прямая, параллельная стороне треугольника и проходящая через его середину, является его средней линией.
Существуют равные и подобные треугольники. Для доказательства равенства и подобия используют признаки. Например, треугольники подобны, если углы одного соответственно равны углам другого. Кроме того, любые прямоугольные треугольники с парой равных острых углов подобны.
Скорее всего в условии пропущены слова "Запишите в виде десятичных дробей".
Поэтому:
1) четыре единицы, шесть десятых, восемь сотых - это число 4,68;
2) две единицы, пять сотых - это число 2,08;
3) восемь тысяч, три единицы, семь сотых, восемь десятитысячных - это число 8 003,0708;
4) три десятка, две десятых, девять стотысячных - это число 30,2009;
5) одна сотня тысяч, одна стотысячная - 100 000,00001.
Нужно знать названия разрядов чисел:
..., сотни тысяч, десятки тысяч, единицы тысяч, сотни, десятки, единицы, десятые, сотые, тысячные, десятитысячные, стотысячные, ...
Например, 456 567,678943 - можно прочитать так:
4 сотни тысяч 5 десятков тысяч, 6 еиниц тысяч, 5 сотен, 6 десятков, 7 единиц, 6 десятых, 7 сотых, 8 тысячных, 9 стотысячных, 4 миллионных 3 десятимиллионных.