1. Какую цель преследовал Александр Македонский при завоевании нашей Родины?
2. Что вы узнали о восстании во главе со Спитаменом, боровшимся за
свободу Отчизны?
3. Каким путём Александр Македонский победил Спитамена?​

КЕ = 2,8 ед.

Пошаговое объяснение:

Косинус угла в прямоугольном треугольнике - это отношение прилежащего катета к гипотенузе.

Из треугольников ВЕС и АКС имеем:

CosC = ЕС/ВС и CosC = КС/АС  соответственно.

Так как ЕС/ВС = КС/АС = 0,4, а угол С у них общий, следовательно треугольники АВС и ЕКС подобны по признаку: "Если две стороны одного треугольника пропорциональны двум сторонам другого треугольника, а углы, заключённые между этими сторонами равны, то такие треугольники подобны". Коэффициент подобия этих треугольников равен k = 0,4. Тогда

КЕ = АВ·k = 7·0,4 = 2,8 ед.

Перевод:

а) Скорость орла в секунду - 30 м. Сколько метров он пролетает за 5 с? б) Улитка переместилась на 36 м за 2 часа. Какая скорость улитки?

в) Велосипедист проехал 28 км со скоростью 14 км/ч. Как долго он проезжал этот путь?

--------------------------------------------------------------------------------------------------------

Формулы использованные в задачах:

а)

Условие:

Скорость орла в секунду - 30 м. Сколько метров он пролетает за 5 с?

Формула: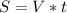

30×5=150 (м)-пролетает орёл за 5 секунд.

ответ: 150 метров.

б)

Условие:

Улитка переместилась на 36 м за 2 часа. Какая скорость улитки?

Формула: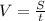

36÷2=18 (м/ч)-скорость улитки.

ответ: 18 м/ч.

в)

Условие:

Велосипедист проехал 28 км со скоростью 14 км/ч. Как долго он проезжал этот путь?

Формула: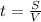

28÷14=2 (часа)-ехал велосипедист.

ответ: 2 часа.