1. Материальная точка движется вдоль прямой по закону s(t)=lnts(t)=lnt. Найти скорость этой точки в момент времени t=3t=3. 2. ABCDA1B1C1D1 - прямоугольный параллелепипед. Расстояние от вершины B1 до диагонали BD равно длине отрезка
3.Из вазы, в которой лежат 4 апельсина и 3 яблока, не глядя берут один плод. Какова вероятность того, что взят апельсин?
4. Объём цилиндра равен 5 см3. Если площадь боковой поверхности цилиндра равна 4 см2, то радиус его основания равен
5.Основание прямой призмы АВСA1B1C1 равнобедренный треугольник АВС, в котором АВ = АС = 10 см и ВС = 12 см. Высота призмы равна 6 см. Площадь сечения этой призмы плоскостью, проходящей через точки A1, С, В будет равна
2) 30,3 км/ч - 1,5 км/ч = 28,8 км/ч - удвоенная скорость первого
3) 28,8 км/ч : 2 = 14,4 км/ч - скорость первого
4) 14,4 км/ч + 1,5 км/ч = 15,9 км/ ч - скорость второго
ответ: 14,4 км/ч; 15,9 км/ч
1) 15,15 км : 0,5 ч = 30,3 км/ч - скорость сближения (т.е. сумма скоростей)
2) 30,3 км/ч + 1,5 км/ч = 31,8 км/ч - удвоенная скорость второго
3) 31,8 км/ч : 2 = 15,9 км/ч - скорость второго
4) 15,9 км/ч - 1,5 км/ч = 14,4 км/ ч - скорость первого
ответ: 14,4 км/ч; 15,9 км/ч
Пошаговое объяснение:
Основная логика решения заключаеться в том, что нам нужно упростить выражение, иначе мы его не посчитаем. Для этого можно присмотреться к степеням, и увидеть что они кратны 7 . Тогда получаеться:
1)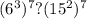
Так как у нас есть общая степень 7, то мы можем ее не учитывать при сравнении. Из этого следует, что нам нужно сравнивать:
2)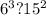
Если на этом этапе вы можете точно определить, какое число больше, значит задача решена, но для тех кто не уверен, можно пойти дальше. Выражения с обеих сторон можно представить в виде произведений с одинаковыми степенями:
3)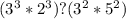
Теперь видно, что у нас есть пара степенных выражений с общим основанием, и мы можем их легко сравнить:
4)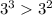
Теперь мы знаем, что первая часть левого выражения больше первой правого. Дальше нам нужно сравнить вторые части обоих выражений, а тут уже нужно вспомнить таблицу умножения:
5)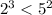
Мы видим, что первое сравнение и второе не совпадают по знаку, тогда берем большее выражение из обоих неравенств и сравниваем между собой:
6)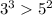
Из этого следует что: