Математика: 1. Найдите область определения функций f(x) 2 исследовать функцию на четность и нечётность

1. Найдите область определения функций f(x) $\frac{2x + 3}{3x {}^{2} - 6x}$

2 исследовать функцию на четность и нечётность

$\frac{5 {x}^{3} }{3x { +}^{4 } +7 }$

Показать ответ

Ответ:

odarka1596

21.02.2020 03:47

Рассмотрим немного другую задачу. Выбрасываются k (k>0) кубиков, человек загадывает число от 1 до 6. Найти вероятность того, что число присутствует хотя бы на одном из кубиков

Событие А="число присутствует хотя бы на одном из кубиков" противоположно событию В="число не присутствует ни на одном из кубиков". Тогда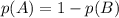 p(A)=1-p(B)

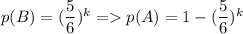Вероятность не угадать число на одном кубике равна $\dfrac{5}{6}$ (среди 6 чисел 5 не подойдут). Тогда вероятность не угадать число на k кубиках равна $p(B)=(\dfrac{5}{6})^k=p(A)=1-(\dfrac{5}{6})^k$ - это и есть искомая вероятность в данной задаче.

Вернемся к исходной задаче. На 1ом этапе вероятность угадать число равна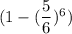 $(1-(\dfrac{5}{6})^6)$ . При условии угадывания числа, на следующем этапе остается 6-1=5 кубиков. Тогда вероятность угадывания на 2ом этапе равна 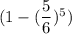$(1-(\dfrac{5}{6})^5)$ . При условии угадывания числа, на следующем этапе остается 5-1=4 кубиков. И т.д. На последнем этапе останется 2 кубика, и вероятность угадывания будет равна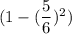 $(1-(\dfrac{5}{6})^2)$

Тогда искомая вероятность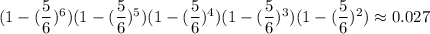 $(1-(\dfrac{5}{6})^6)(1-(\dfrac{5}{6})^5)(1-(\dfrac{5}{6})^4)(1-(\dfrac{5}{6})^3)(1-(\dfrac{5}{6})^2)\approx 0.027$

0,0(0 оценок)

Ответ:

оля2053

21.02.2020 03:47

ответ: p=178/297.

Пошаговое объяснение:

Событие А - студенту досталась задача повышенной сложности - может произойти вместе с одним из событий A1 и A2, называемых гипотезами:

A1 - преподаватель переложил из второго конверта в третий простую задачу:

А2 - задачу повышенной сложности.

Тогда по формуле полной вероятности P(A)=P(A1)*P(A/A1)+P(A2)*P(A/A2).

Но P(A/A1)=6/11, а P(A/A2)=7/11. Остаётся найти P(A1) и P(A2). Заметим сразу, что так как события A1 и A2 несовместны и притом образуют полную группу, то P(A1)+P(A2)=1, откуда P(A2)=1-P(A1). Событие A1 может произойти совместно с одной из 4-х гипотез:

H1 - преподаватель переложил из первого конверта во второй две простых задачи;

H2 - две задачи повышенной сложности;

H3 - простую и повышенной сложности;

H4 - повышенной сложности и простую.

Тогда по формуле полной вероятности P(A1)=P(H1)*P(A1/H1)+P(H2)*P(A1/H2)+P(H3)*P(A1/H3)+P(H4)*P(A1/H4). Но P(H1)=8/12*7/11=56/132=14/33; P(H2)=4/12*3/11=12/132=3/33; P(H3)=8/12*4/11=32/132=8/33; P(H4)=4/12*8/11=32/132=8/33; P(A1/H1)=8/18; P(A1/H2)=6/18; P(A/H3)=P(A/H4)=7/18.

Отсюда P(A1)=121/297 ⇒P(A2)=1-121/297=176/297 и тогда P(A)=121/297*6/11+176/297*7/11=178/297.

0,0(0 оценок)

Популярные вопросы: Математика