1. Найти общее решение дифференциального уравнения с разделяющимися переменными.
А) xy'-y=0
Б)yy'+x=0
2. Найти частное решение дифференциального уравнения с разделяющимися переменными.
tg(x)*y'=1+y если x=П/6; y=-1/2
3.Найти решение однородного дифференциального уравнения первого порядка.
yy'=2y-x
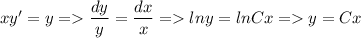
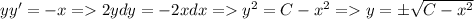
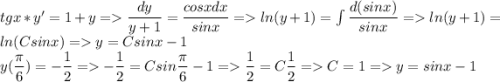
![yy'=2y-x\\ \left[y=x*u(x)=y'=\\ u+xu'\right]\\ xu(u+xu')=2xu-x\\ xu'=2-\dfrac{1}{u}-u\\ \int\dfrac{-udu}{(u-1)^2}=\int\dfrac{dx}{x}\\ -\int\dfrac{((u-1)+1)du}{(u-1)^2}=lnCx\\ \int\dfrac{du}{(u-1)}+\int\dfrac{du}{(u-1)^2}=-lnCx\\ ln(u-1)-\dfrac{1}{u-1}=-lnCx\\ ln(\dfrac{y}{x}-1)-\dfrac{x}{y-x}=-lnCx](/tpl/images/1083/4240/69b13.png)