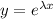1. Найти общее решение дифференциального уравнения с разделяющимися переменными: y'=ycosx 2. Решить линейное дифференциальное уравнение первого порядка: y'= $\frac{2x}{1+2x^{x} } y=\frac{2x^{2} }{1+x^{2} }$ 3. Решить линейное однородное дифференциальное уравнение 2-го порядка с постоянными коэффициентами: y"=-6y'+13y=0

Показать ответ

Ответ:

Adriet

15.10.2020 14:59

$1)~ y'=y\cos x\\ \\ \frac{dy}{dx}=y\cos x\\ \\ \int \frac{dy}{y}=\int \cos xdx\\ \\ \ln|y|-\ln C=\sin x\\ \\ y=C\sin x$

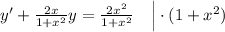
2) $y'+\frac{2x}{1+x^2}y=\frac{2x^2}{1+x^2}~~~\Big|\cdot (1+x^2)$

$y'\cdot (1+x^2)+y\cdot 2x=2x^2\\ \\ \Big(y\cdot (1+x^2)\Big)'=2x^2\\ \\ y\cdot (1+x^2)=\int 2x^2dx\\ \\ y\cdot (1+x^2)=\frac{2x^3}{3}+C\\ \\ y=\frac{(2x^3/3)+C}{1+x^2}$

3) Пусть $y=e^{\lambda x}$

$\lambda^2-6\lambda+13=0\\\\ (\lambda-3)^2+4=0\\ \\ \lambda=3\pm 2i$

$y=e^{3x}\cdot \Big(C_1\cos 2x+C_2\sin 2x\Big)$

0,0(0 оценок)

Популярные вопросы: Математика

Alisa11221122

19.11.2022 16:49

Выполните деление : 2 ) 6 целых ÷ 1 / 11 4 ) 5 целых ÷ 5 / 7 6) 10 целых ÷ 5/8...

Anabella98

19.11.2022 16:49

Выполни умножение смешаногочисла на натуральное 3 1/4*8...

danilchirkov0

19.11.2022 16:49

На просмотр фильма с двух классов пришла одинаковая сумма людей. с первого класса было 12 девочек, а со второго на 25% больше. мальчиков из первого класса было на...

hiphoptema01

19.11.2022 16:49

На базу 6машин картофеля по 65ц в каждой. отправили в магазин 2/5 части всего картофеля. сколько ц картофеля осталось на базе?...

LOKI46

13.11.2020 22:33

Водной пачке 1/4 кг урюка в скольких пакетах содержится 6 кг урюка....

Levkoi

13.11.2020 22:33

Каждую головку сыра продавец разрезал пополам а каждую половинку ещё пополам . сколько было головок сыра если всего получилось 12 кусков...

fjdjwjqksnddjj

13.11.2020 22:33

Решить пример 2 целых 1/12 * 4 целых 4/5...

vlad1458

13.11.2020 22:33

Найдите значения выражений при а + б = 260 пример (а+70)+b ответ...

RomaAksenov2007

13.11.2020 22:33

Составьте по уравнению икс минус пять седьмых равно одна седьмых...

vikabosch

13.11.2020 22:33

Укажи все делители числа 1,48,100,104,121,256....

Полный доступ

Позволит учиться лучше и быстрее. Неограниченный доступ к базе и ответам от экспертов и ai-bota Оформи подписку