1.осьовий переріз циліндра – квадрат, сторона якого дорівнює 5 дм. знайдіть довжину кола основи циліндра
2.радіус основи циліндра дорівнює 3см, а його висота – 4 см. знайдіть об’єм циліндра.
3.висота циліндра дорівнює 6 см, а діаметр його основи – 8 см. знайдіть площу повної поверхні циліндра
,!

Игорь Федорович Стравинский вышел из школы Римского-Корсакова, впитал традиции русской классики — Глинки, «Могучей кучки», Чайковского, был взращен эпохой общественного подъема и культурного расцвета России в 900-е годы. Один из самых ярких представителей русской музыки предреволюционного десятилетия, Стравинский после его отъезда из России (1913) стал общепризнанным лидером зарубежной музыки и в значительной мере определял — по крайней мере, от «Весны священной» (1913) до Requiem Canticles (1966) — музыкальный процесс XX века.

Творческий путь Стравинского пролегал в мире, который потрясали Октябрьская революция, Первая и Вторая мировые войны. И композитор жил, по его признанию, con tempo (со временем). Его музыка отразила как бури и противоречия века, так и мечту о гармонии, эстетическом порядке.

После шестидесяти лет активной творческой работы Стра­винский оставил колоссальное творческое наследие, а его эволюция отличалась необычайной сложностью. Внешняя многоликость его композиторской манеры давала, казалось бы, повод для упреков в изменчивости творческого облика, в своеобразном «протеизме», но за этой изменчивостью нельзя не почувствовать внутреннего единства стиля и его русской сущности как постоянной доминанты.

Особая тема — Стравинский и мировая музыка. Его воздей­ствие испытали представители и «молодых», и «древних» му­зыкальных культур: венгр Барток, чех Мартину, испанец де Фалья, мексиканец Чавес, бразилец Вила-Лобос, компози­торы Франции — Онеггер, Мийо, Пуленк, Мессиан, Булез, немцы Хиндемит и Орф, итальянцы Казелла и Малипьеро, музыканты США, Англии... Все они учились у Стравинского обращению с фольклором, ритмической технике и технике остинато, политональным и полиладовым сочетаниям, оркест­ровому и ансамблевому письму.

У Стравинского восприняли немало и отечественные компо­зиторы — Шостакович, Прокофьев, Щедрин, Слонимский, Шнитке, Гаврилин, Пригожин. Без завоеваний Стравинского, свободно оперировавшего стилями разных эпох, немыслима современная техника полистилистики, к которой обращаются Берио и Шнитке, Щедрин и Пендерецкий.

Стравинский — и в пору «Русских сезонов» Дягилева, и позднее — активно мировому распространению и росту престижа русской музыки.

ДАНО

Y = (x² + 9)/x

ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота:  Х= 1. 
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота 
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.

6. Проверка на чётность.
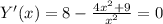
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.

6. Локальные  экстремумы.
Y'(x) = 0,  x1 = - 3/2,  x2 = 3/2
Максимум Y(-3/2)= .-12.

Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).

Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.

Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)

10. График в приложении