1)Отметить на координатной оси единичный отрезок 5 клеток. Отметить числа ⅕, ⅖, ⅗, ⅘, -⅕, -⅖, -⅗, -⅘. 2. 2)Отметить на координатной оси удобный единичный отрезок и отметить числа ½,⅔, -⅚, -³/2.
Нам необходимо перемножить две десятичные дроби. Для начала представим их в виде неправильных дробей:
- в данной дроби 25 целых и 45 сотых. Запишем это в виде дроби с целой частью:
Для удобства, мы можем сократить дробную часть на 5 в числителе и знаменателе:
Теперь переведем в неправильную дробь:
Далее, разберемся с дробью . Запишем ее в виде: , сократим числитель и знаменатель на 2: .
Теперь запишем произведение двух преобразованных дробей:. Имеем право сократить числитель второй дроби со знаменателем первой, получим: .
Получили неправильную дробь, из которой нужно выделить целую часть. В 509 20 целых частей, так как ближайшее число, которое делится на 25, это 500, а 9 получаем в остатке. Запишем:
Чтобы вернуться обратно в десятичную дробь, необходимо знаменатель домножить на 4, чтобы он стал равен 100, получим:
Пошаговое объяснение:
Нам необходимо перемножить две десятичные дроби. Для начала представим их в виде неправильных дробей:
Для удобства, мы можем сократить дробную часть на 5 в числителе и знаменателе: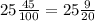
Теперь переведем в неправильную дробь:
Далее, разберемся с дробью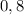 . Запишем ее в виде:
. Запишем ее в виде:  , сократим числитель и знаменатель на 2:
, сократим числитель и знаменатель на 2:  .
.
Теперь запишем произведение двух преобразованных дробей: . Имеем право сократить числитель второй дроби со знаменателем первой, получим:
. Имеем право сократить числитель второй дроби со знаменателем первой, получим:  .
.
Получили неправильную дробь, из которой нужно выделить целую часть. В 509 20 целых частей, так как ближайшее число, которое делится на 25, это 500, а 9 получаем в остатке. Запишем:
Чтобы вернуться обратно в десятичную дробь, необходимо знаменатель домножить на 4, чтобы он стал равен 100, получим:
за 8 с Иван 50 м
Пошаговое объяснение:
Естественно, скорости всех бегунов разные. Обозначим их вот так:
V₁, V₂, V₃, V₄, V₅ < Vи, где Vи - скорость Ивана. Все скорости в м/с
запишем формально все известные нам данные:
1. Через 8 с суммарное расстояние 280 м:
8(V₁+V₂+V₃+V₄+V₅+Vи)=280;
2. Когда Иван финишировал... А когда (через сколько секунд) Иван финишировал? А Иван пробежал 100 м со своей (постоянной!) скоростью за tи, с:
tи[с]=100[м]/Vи[м/с]
А что нам известно про этот момент времени? А вот что. Бегунам-неудачникам осталось суммарно пробежать 40 м (из 500 суммарных):
100/(Vи)*(V₁+V₂+V₃+V₄+V₅)=500-40
Итак имеем два уравнения. Это хорошо, хотя переменных слишком много... Покрутим их с Алгебры:
8(V₁+V₂+V₃+V₄+V₅+Vи)=280;
100/(Vи)*(V₁+V₂+V₃+V₄+V₅)=460;
Из второго уравнения сумму скоростей четверых бегунов:
V₁+V₂+V₃+V₄+V₅=460*Vи/100; ⇒ V₁+V₂+V₃+V₄+V₅=4.6*Vи
и в первое (немножко преобразуем первое перед этим):
8Vи+8(V₁+V₂+V₃+V₄+V₅)=280; ⇒ 8Vи+8*4.6*Vи=280;
ну вот, одно уравнение с однми неизвестным. Да здравствует алгебра!
8Vи+8*4.6*Vи=280;
Vи(8+8*4,6)=280;
Vи=280/(8+8*4,6);
Vи=6.25 [м/с] - скорость Ивана!
Ну, а за 8 с Иван пробежал 6.25*8=50 [м]