1 Площадь основания прямоугольного параллелепипеда равна 24 см2. Одна из сторон основания равна 3 см,
высота равна половине периметра основания. Найти площадь боковой поверхности.
2 Основанием прямой призмы служит прямоугольный треугольник, катеты которого равны 5 и 12 см. Высота
призмы 2 см. Найти площадь полной поверхности призмы.
3 В правильной пирамиде диагональ основания равна 4
2 см, апофема равна 5 см. Найти высоту пирамиды.
4 Площадь осевого сечения цилиндра равна 35 см2, площадь основания 25π см2. Найти площадь боковой
поверхности цилиндра.
5 Осевым сечение конуса является прямоугольный треугольник, гипотенуза которого равна 8
2 . Найти площадь
боковой поверхности.
6 Основание прямой призмы – прямоугольный треугольник, с гипотенузой 13 см и катетом 12 см. Найдите
площадь боковой поверхности призмы, если ее наименьшая боковая грань квадрат.
urok_tehnologiya_5_klassk_i_ego_ustroystvo.szhat_
Основным оборудованием рабочего места в школьной мастерской является специальный стол — верстак. Для ручной обработки древесины используется столярный верстак. Он состоит из двух частей: подверстачье (опора верстака) и верстачная доска (рабочая часть). Для закрепления заготовки служат при верстака:
передний и задний винтовой зажим, а также гнезда с клиньями (колышками). Для хранения инструментов служит лоток — углубление в середине верстака. В зажиме верстака используется винтовой механизм (винт и гайка). С его (вращением рукоятки ходового винта, которое вызывает перемещение прижимного бруска) можно закреплять или освобождать деталь.
Дано:
∠
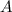
Выяснить: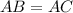
или 
.
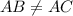Решение.
1) Рассмотрим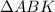
и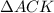 
.
У них:
∠
=∠
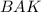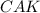, как половинки ∠
;
∠
= ∠
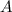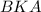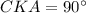как углы, образованные
перпендикулярными прямым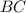и
и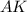 
;
Таким образом, сторона и два прилежащих к ней угла одного треугольника равны стороне и двум прилежащих к ней углам другого треугольника, а это означает, что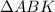
= 
.
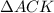2) Из равенства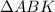
и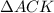 
следует равенство соответственных сторон: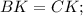 
и соответственных углов ∠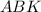
=∠
.
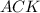=> Δ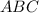
- равнобедренный.
ответ: да, можно.