1. прямая у=5х+3 является касательной к графику функции у=х (в квадрате) +3х+4. найдите абсциссу точки касания 2. найти меньший корень уравнения : (см.фото)
1) Касательная к параболе всегда имеет только одну общую точку. Поэтому, если мы решим уравнение
, то окажется, что тут только один корень.
. И понятное дело, что говорится о точке x = 1
2)
Аргумент логарифма должен быть строго больше нуля, поэтому найдем ОДЗ уравнения:
Решая по методу интервалов, мы придем к тому, что x, не входя в интервал [-1; 0], может быть любым
Теперь решаем уравнение:
По теореме Виета корни очень легко подобрать: это 1 и -2. Оба корня удовлетворяют ОДЗ, о котором мы говорили выше, но нужно найти наименьший корень, а это -2. Поэтому ответом будет -2.
1) x = 1
2) x = -2
Пошаговое объяснение:
1) Касательная к параболе всегда имеет только одну общую точку. Поэтому, если мы решим уравнение
, то окажется, что тут только один корень.
2)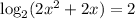
Аргумент логарифма должен быть строго больше нуля, поэтому найдем ОДЗ уравнения:
Решая по методу интервалов, мы придем к тому, что x, не входя в интервал [-1; 0], может быть любым
Теперь решаем уравнение:
По теореме Виета корни очень легко подобрать: это 1 и -2. Оба корня удовлетворяют ОДЗ, о котором мы говорили выше, но нужно найти наименьший корень, а это -2. Поэтому ответом будет -2.
1. 1.
2. - 2.
Пошаговое объяснение:
1. у=х^2+3х+4, угловой коэффициент касательной к равен 5.
у' = 2х + 3
По условию у'(хо) =к, тогда
2•х0 + 3 = 5
2х0 = 5 - 3
2х0 = 2
х0 = 1
1 - абсцисса точки касания.
2. log(2)(2x^2+2x) = 2
ОДЗ: 2x^2+2x > 0
2x(x + 1)>0
_+__(-1)__-__(0)__+___
2x^2+2x = 2^2
2x^2+2x = 4
2x^2 + 2x - 4 = 0
х^2 + х - 2 = 0
D = 1 + 8 = 9
x1 = ( -1+3)/2 = 1;
x2 = ( -1-3)/2 = -2;
Оба корня входят в ОДЗ.
-2 - меньший корень уравнения.