1) Раскройте скобки и упростите выражение 1. x-(x -y)
2. a - (b + a)
3. (m - n ) + n
4. (x + y) - y
5. 5– (3 + x)
6. – x + (x + 2,7)
7. – (– в + 3,8) + 0,7
8. 4,74 – ( 2а + 3,7)
1) Раскройте скобки и упростите выражение
1. - (1 - x) - (5,1 + x)
2. - (a - x - 3) - (x - a + 2)
3. (a + 3,3 - a) - (3,3 + x)
4. (c + 4,9) - (5,4 + c)
5. (n - 5,8) - (4,9 + n)
6. (6,08 + a) - (a + 9,3)
7. - (m - 3,8) + (4,12 + m)
8. - (2,43 + x - b) - (2,43 + b - x)
9. - (1,53 - x + 1) - (x - a - 2,53)
10. - (a - x) - (5,1 + x) + a - 5,1
11. (b - x) - (a - x) + (a - b)
12. - (a + 3,3) - (x - a) - 3,3 + x
13. (2,43 + 1,1) - (b + 2,43) + (b - 1,1)
14. (1,53 - x + a) - (x - 1,53 - a) - a
15. - (a - 1,21) - (1 - a) - (0,21 - a)
3) Раскройте скобки и найдите значение выражения.
1. 128 + (224 – 28)
2. 397 – (25 + 197)
3. 1203 – (–154 + 803)
4. 10005 + (–12005 + 876)
5. 9054 – (+32 – 2046)
6. 1212 + (+9888 + 279)
7. –812 – (–112 – 524)
8. – ( 725 + 128 – 275) + 972
4) Вычислите
1. 108-(108-5)=
2. -56+(-98+56)=
3. (79-81)-(39-81)=
4. (-39+15)-(5-39)=
5. -49-(-49+2)=
6. 100-(-5+100)=
5) Решите уравнения, предварительно раскрыв скобки
1. 12 + (x – 4 ) = 56
2. 85 – (– 18 – y) = 76
3. –906 – (36 + k) = – 120
Это 6 класс
33
Пошаговое объяснение:
Треугольник, у которого все три стороны равны, называется равносторонним (или правильным) треугольником.
Обозначим сторону данного по условию треугольника как a. Так как периметр многоугольника равен сумме длин всех его сторон, то периметр равностороннего треугольника, данного по условию равен:
P = a + a + a = 33 * a.
Так как сумма сторон треугольника с тремя равными сторонами равна 99 см, то его периметр равен также 99 см. Таким образом:
33 * a = 99;
a = 99/33 (по пропорции);
a = 33 см.
ответ: сторона треугольника, у которого все три стороны равны, и сумма которых равна 99 см, равна 33 см.
7.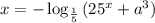
Пусть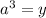 , количество корней от этого не изменится.
, количество корней от этого не изменится.
Рассмотрим функцию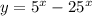 :
:
До точки экстремума функция возрастает, а после — убывает. Значит, это точка максимума. Максимальное значение функции равно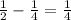 . Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
. Прикинем график функции (см. рис. 1). Уравнение имеет 2 различных решения, если:
ответ:![(0; \frac{\sqrt[3]{2}}{2})](/tpl/images/0445/7312/80965.png)
8. При изменении размеров пирамиды соотношения между соответственными элементами не изменятся, поэтому примем для простоты вычислений сторону основания за 1.
Рассмотрим первую пирамиду:
Пусть SKM — сечение пирамиды SABCD, где K и M — середины BC и AD соответственно. Тогда в это сечение попадает окружность, вписанная в треугольник SKM и касающаяся KM в точке S' (проекция точки S), SK в точке K'. Пусть ∠SKS' = α, KO₁ — биссектриса, тогда:
Учитывая, что угол находится в первой четверти,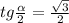
Рассмотрим вторую пирамиду:
Пусть S₁A₁C₁ — сечение пирамиды S₁A₁B₁C₁D₁. Это сечение содержит окружность, вписанную в треугольник S₁A₁C₁, касающуюся стороны A₁C₁ в точке S₁' (проекция точки S₁) и стороны S₁A₁ в точке A₁'. Пусть ∠S₁A₁S₁' = β, A₁O₂ — биссектриса. Тогда:
Решая аналогичное уравнение, получаем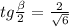
ответ: 4 : 3