1.В двух кучках 42 камушка,при этом в первой кучке их на 8 больше,чем в другой. Сколько камушков в каждой кучке? 2. Сумма 4 последовательных целых чисел равна 58. Найдите эти числа.
Задача №1. Пусть камушков лежало во 2 кучке, тогда в 1 кучке лежало камушков. В 2 кучах всего лежит камушка.
Составим и решим уравнение по данным условиям:
Значит всего во 2 кучке лежало камушков. Но это только часть ответа к нашей задаче!
Мы нашли кол-во камушков только во 2 кучке, а у нас есть ещё и 1 кучка! Мы сможем это сделать, подставив в выражение для 1 кучки, которое мы составляли для уравнения, значение .
Т.е. камешков лежало в 1 кучке.
Проверка:
камушка в 2 кучках (задаче решена верно).
Вот теперь можно сказать, что: Задача решена! ☑
ответ: в 1 кучке лежало камушков, а во 2 кучке камушков.
Задача №2. Пусть первое целое число, тогда если числа последовательные, то следующие 3 целых числа буду равны , и . Их сумма равна .
Составим и решим уравнение по данным условиям:
Значит 1 целое число равно . Но это снова только часть ответа к нашей задаче!
Мы нашли только 1 целое число, а нам нужно узнать ещё и 2, и 3, и 4. Мы сможем это сделать, подставив в каждое выражение, составленное для 2, 3 и 4 числа к уравнению, значение . То есть:
Составим и решим уравнение по данным условиям:
Значит всего во 2 кучке лежало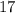 камушков. Но это только часть ответа к нашей задаче!
камушков. Но это только часть ответа к нашей задаче!
Мы нашли кол-во камушков только во 2 кучке, а у нас есть ещё и 1 кучка! Мы сможем это сделать, подставив в выражение для 1 кучки, которое мы составляли для уравнения, значение .
.
Т.е.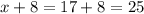 камешков лежало в 1 кучке.
камешков лежало в 1 кучке.
Проверка:
Вот теперь можно сказать, что: Задача решена! ☑
ответ: в 1 кучке лежало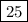 камушков, а во 2 кучке
камушков, а во 2 кучке  камушков.
камушков.
Задача №2. ПустьСоставим и решим уравнение по данным условиям:
Значит 1 целое число равно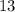 . Но это снова только часть ответа к нашей задаче!
. Но это снова только часть ответа к нашей задаче!
Мы нашли только 1 целое число, а нам нужно узнать ещё и 2, и 3, и 4. Мы сможем это сделать, подставив в каждое выражение, составленное для 2, 3 и 4 числа к уравнению, значение . То есть:
. То есть:
Проверка:
Вот теперь можно сказать, что: Задача решена! ☑
ответ: 1 число -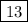 , 2 число -
, 2 число -  , 3 число -
, 3 число - 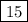 , 4 число -
, 4 число - 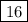 .
.