1. В равнобедренной трапеции АВСД сторона АД параллельна стороне ВС, угол А равен 30 градусов, высота ВК равна 1 см, сторона ВС равна 4 см. а) Найдите площадь трапеции. б) Найдите площадь треугольника КДМ, если точка М –середина отрезка ВД.
Пусть х это сторона квадрата Тогда периметр равен Р=х+х+х+х=4х вырази сторону через периметр Р=4х Х=Р/4 площадь квадрата равна S1=x*x=x^2 выразить площадь через периметр, S1=x^2=(P/4)^2=P^2/16
периметр был 100% а стал 100%+10%=110% совсем пропорцию
Р1—100% Р2—110%
Р2=110%*H1/100%=1.1Р1
Тогда подставим значение данного периметра в формулу площади
S2=P^2/16=(1.1P)^2/16=1.21P^2/16 Составим пропорцию P1^2/16 это 100% 1.21Р1/16 это у %
У=1.21Р^2*100/16: Р^2/16=121Р^2/16*16/Р^2=(121Р^2*16)/(16*Р^2)=121 Значит было 100% а стало 121% тогда разница равна 121%-100%=21% ответ увеличилась на 21%
Мы знаем что периметр квадрата это сумма длин всех его сторон.
Если одна сторона равна "х", то периметр равен:
Р квадрата = х+х+х+х= 4х
Площадь квадрата это произведение двух его сторон (независимо каких, потому что у него все стороны равны):
S квадрата =
В условии нам сказали:
"На сколько процентов увеличится площадь квадрата если его периметр увеличится на 40%?"
Переводим 40% в дробь:
40%=40:100=0,4.
Увеличиваем периметр на 40% (0,4) :
4х*0,4=1,6х (см)-на столько увеличится периметр.
А нам нужно узнать размер периметра, при увеличении на 40%, мы уже нашли эти 40%, поэтому нам нужно к периметру, который был изначально (до его увеличения на 40%) прибавить 40%, мы их уже нашли (1,6х):
4х+1,6х=5,6х (см)-периметр после его увеличения на 40%.
Теперь мы с периметра сможем найти одну сторону, раз у квадрата все стороны (4) равны, то нам нужно периметр (5,6х) разделить на количество сторон (4):
5,6х:4=1,4х (см)-это одна сторона этого квадрата (после увеличения его периметра на 40%).
Итак, мы знаем одну сторону квадрата, у которого увеличили периметр на 40%. Теперь мы можем найти площадь увеличенного квадрата.
Ещё раз повторяю что площадь квадрата это произведение двух его сторон (независимо каких, потому что у него все стороны равны):
S квадрата = -это площадь увеличенного квадрата.
Теперь из большей площади квадрата( ) вычитаем меньшую площадь квадрата ():
Переведём дробь в проценты:
0,96*100=96%
Значит на 96% увеличится площадь квадрата если его периметр увеличится на 40%.
Тогда периметр равен Р=х+х+х+х=4х
вырази сторону через периметр
Р=4х
Х=Р/4
площадь квадрата равна
S1=x*x=x^2
выразить площадь через периметр,
S1=x^2=(P/4)^2=P^2/16
периметр был 100% а стал 100%+10%=110%
совсем пропорцию
Р1—100%
Р2—110%
Р2=110%*H1/100%=1.1Р1
Тогда подставим значение данного периметра в формулу площади
S2=P^2/16=(1.1P)^2/16=1.21P^2/16
Составим пропорцию
P1^2/16 это 100%
1.21Р1/16 это у %
У=1.21Р^2*100/16: Р^2/16=121Р^2/16*16/Р^2=(121Р^2*16)/(16*Р^2)=121
Значит было 100% а стало 121% тогда разница равна
121%-100%=21%
ответ увеличилась на 21%
На 96%.
Пошаговое объяснение:
РЕШЕНО МУДROSTПусть х - это одна сторона квадрата.
Мы знаем что периметр квадрата это сумма длин всех его сторон.
Если одна сторона равна "х", то периметр равен:
Р квадрата = х+х+х+х= 4х
Площадь квадрата это произведение двух его сторон (независимо каких, потому что у него все стороны равны):
S квадрата =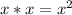
В условии нам сказали:
"На сколько процентов увеличится площадь квадрата если его периметр увеличится на 40%?"
Переводим 40% в дробь:
40%=40:100=0,4.
Увеличиваем периметр на 40% (0,4) :
4х*0,4=1,6х (см)-на столько увеличится периметр.
А нам нужно узнать размер периметра, при увеличении на 40%, мы уже нашли эти 40%, поэтому нам нужно к периметру, который был изначально (до его увеличения на 40%) прибавить 40%, мы их уже нашли (1,6х):
4х+1,6х=5,6х (см)-периметр после его увеличения на 40%.
Теперь мы с периметра сможем найти одну сторону, раз у квадрата все стороны (4) равны, то нам нужно периметр (5,6х) разделить на количество сторон (4):
5,6х:4=1,4х (см)-это одна сторона этого квадрата (после увеличения его периметра на 40%).
Итак, мы знаем одну сторону квадрата, у которого увеличили периметр на 40%. Теперь мы можем найти площадь увеличенного квадрата.
Ещё раз повторяю что площадь квадрата это произведение двух его сторон (независимо каких, потому что у него все стороны равны):
S квадрата =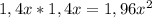
-это площадь увеличенного квадрата.
Теперь из большей площади квадрата(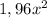
) вычитаем меньшую площадь квадрата (
):
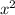Переведём дробь в проценты:
0,96*100=96%
Значит на 96% увеличится площадь квадрата если его периметр увеличится на 40%.
РЕШЕНО МУДROST