Не увидела связи между прямоугольником и рассматриваемым. потому решение может не очень красивое.
Заметим, что есть узловая точка , которая делит прямоугольник на два (по диагонали), в которых количества пересекаемых квадратиков равны и потому можно посчитать только в одном из них.
Рассмотрим две горизонтальные прямые и диагональ. Внутри они образуют прямоугольный треугольник, один из катетов которого (горизонтальный) равен . Ну а тогда второй равен , а потому количество пересекаемых квадратов в каждой из горизонталей либо , либо . Поймем, когда их три.
Три квадратика образуются тогда и только тогда, когда точки пересечения соседних вертикалей находятся между соседними горизонталями. Для этого требуется, чтобы точка ( -- номер вертикали) достаточно далеко находилась от ближайшего целого, то есть дробная часть , что равносильно тому, что , поскольку иначе число дает остаток, не меньший . Но , а потому единственными решениями будут , то есть крайние вертикали, что не подходит. Значит, во всех горизонталях задеваются ровно два квадрата, а значит всего .
Ни один из них не может следить сам за собой. Ни какие двое не могут следить друг за другом. Пусть 001 следит за 003, тогда 003 следит за 002. 002 следит за 001, но тогда 003 следит за тем, кто следит за 001, а не за тем, кто следит за 004. Противоречие. Пусть 001 следит за 004, тогда 004 следит за 002, 002 за 005, 005 за 003, 003 за 001 и одновременно за 006. Противоречие. Пусть 001 следит за 005. Тогда 005 за 002, 002 за 006, 006 за 003, 003 за 007, 007 за 004, 004 за 001. Здесь никаких противоречий нет. ответ: 005 следит за 002.
Не увидела связи между прямоугольником
и рассматриваемым. потому решение может не очень красивое.
Заметим, что есть узловая точка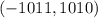
, которая делит прямоугольник на два (по диагонали), в которых количества пересекаемых квадратиков равны и потому можно посчитать только в одном из них.
Рассмотрим две горизонтальные прямые и диагональ. Внутри они образуют прямоугольный треугольник, один из катетов которого (горизонтальный) равен
. Ну а тогда второй равен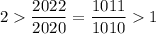 
, а потому количество пересекаемых квадратов в каждой из горизонталей либо 
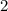, либо 
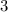. Поймем, когда их три.
Три квадратика образуются тогда и только тогда, когда точки пересечения соседних вертикалей находятся между соседними горизонталями. Для этого требуется, чтобы точка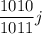
(
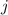-- номер вертикали) достаточно далеко находилась от ближайшего целого, то есть дробная часть 
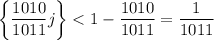, что равносильно тому, что 
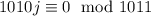, поскольку иначе число 
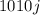дает остаток, не меньший 
. Но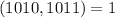 
, а потому единственными решениями будут 
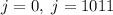, то есть крайние вертикали, что не подходит. Значит, во всех горизонталях задеваются ровно два квадрата, а значит всего 
.
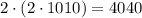Ни какие двое не могут следить друг за другом.
Пусть 001 следит за 003, тогда 003 следит за 002.
002 следит за 001, но тогда 003 следит за тем, кто следит за 001, а не за тем, кто следит за 004. Противоречие.
Пусть 001 следит за 004, тогда 004 следит за 002, 002 за 005,
005 за 003, 003 за 001 и одновременно за 006. Противоречие.
Пусть 001 следит за 005. Тогда 005 за 002, 002 за 006,
006 за 003, 003 за 007, 007 за 004, 004 за 001.
Здесь никаких противоречий нет.
ответ: 005 следит за 002.