1. Вероятность получения выпускником одного места работы равна 0,3, вероятность получения другого места работы 0,1. Какова вероятность получения хотя бы одного места работы?
2. Из трех маршрутов трамваев №8, №10, №15 для служащего попутными являются маршруты №8 и №10. Вычислите вероятность того, что к остановке первым подойдет трамвай попутного маршрута, если по линиям маршрутов №8, №10 и №15курсируют соответственно 7, 9 и 12 вагонов. Протяженность вагонов считается одинаковой.
3. Консультационная фирма претендует на два заказа от двух крупных фирм корпораций. Эксперты фирмы считают, что вероятность получения заказа в первой корпорации 0,45. а у второй 0,9. Какова вероятность, что фирма получит оба заказа?
4. В коробке 24 шара, из них 10 белых и 14 черных. Из коробки вынимают два шара. Найти вероятность того, что оба шара окажутся белыми.
5. У продавца на рынке 60 арбузов, из которых 50 спелых. Покупатель выбирает 2 арбуза. Какова вероятность, что оба арбуза спелые?
6.В коробке 250 ламп, из них 100 по 100 Вт, 50 – 60 Вт, 50 – 15 Вт. Вычислите вероятность того, что мощность каждой лампочки не превысит 60 Вт.

Показать ответ

Ответ:

AnastasiaVolk534

25.03.2021 01:01

Для начала поработаем со вторым выражением. Первые три слагаемых свернем в квадрат разности: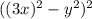 $((3x)^{2}-y^{2})^{2}$ ; В следующих двух слагаемых вынесем общий множитель "40": 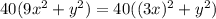$40(9x^{2}+y^{2})=40((3x)^{2}+y^{2})$ ; В итоге получим следующее уравнение: 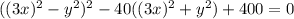$((3x)^{2}-y^{2})^{2}-40((3x)^{2}+y^{2})+400=0$ . В скобках мы видим похожие выражения, отличающиеся лишь знаком посередине (такие выражение называются сопряженными). А хотелось бы видеть там равные (строго говоря тождественные) выражения. Пусть в первой скобке вместо 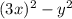$(3x)^{2}-y^{2}$ будет стоять 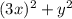$(3x)^{2}+y^{2}$ ; Это приведет к тому, что придется убавить 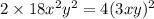$2\times 18x^2y^2=4(3xy)^{2}$ ; В итоге: 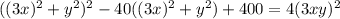$((3x)^{2}+y^{2})^{2}-40((3x)^{2}+y^{2})+400= 4(3xy)^{2}$ ; Слева стоит квадрат суммы. Уравнение примет вид: 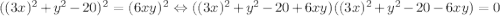$((3x)^{2}+y^{2}-20)^{2}=(6xy)^{2} \Leftrightarrow ((3x)^{2}+y^{2}-20+6xy)((3x)^{2}+y^{2}-20-6xy)=0$ ; Сворачивая еще раз: 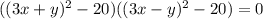$((3x+y)^{2}-20)((3x-y)^{2}-20)=0$ ; Получаем серию прямых: 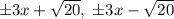$\pm 3x+\sqrt{20},\; \pm3x-\sqrt{20}$ ; А теперь приступим к рассмотрению первого уравнения.

Это уравнение задает круг с центром в точке (0, 0) и радиусом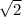 $\sqrt{2}$ ; Рассмотрим прямую 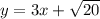$y=3x+\sqrt{20}$ ; Найдем радиус окружности с центром в начале координат, которая касается данной прямой. Это легко сделать из подобия треугольников. 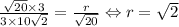$\frac{\sqrt{20}\times 3}{3\times 10\sqrt{2}}=\frac{r}{\sqrt{20}} \Leftrightarrow r=\sqrt{2}$ ; Значит, круг касается всех этих четырех прямых. Достаточно найти только координаты касания с любой из прямых. Это делается так же, как и находился радиус окружности. Для той же прямой это координаты 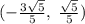$(-\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5} } )$ ; Ну а все решения:

$(\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5}),\; (\frac{3\sqrt{5}}{5},\; -\frac{\sqrt{5}}{5}),\; (-\frac{3\sqrt{5}}{5},\; \frac{\sqrt{5}}{5}),\; (-\frac{3\sqrt{5}}{5},\; -\frac{\sqrt{5}}{5})$