1. Выберите функции, графики которых параллельны: Верных ответов: 2 у = 0,5х + 8 и у=1/3 x+8 . y= 2х-4 и у = -2х + 4 . у= 3/10 х-2 и у 0,3х +5 . у =2/7 + 2 и у = 2 . у= 3x + 6 и у= 3x + 2
(в цепочке равенств оставил только первый и последний член).
Значит после переноса получаем:
.
Теперь работаем с числителем.
.
Значит
.
Осталось самое приятное: подставить наши результаты в дробь, и понять, что всё получилось
ч.т.д.
2)
Перемножим дробь "крест-накрест", получим:
по формуле разностти квадратов, получаем:
переносим в одну часть
,
что верно в силу основного тригонометрического тождества. Так как мы тождественными преобразованиями перешли от исходного выражения к тождественному равенству, значит изначально тоже было тождественное равенство, ч.т.д.
(в цепочке равенств оставил только первый и последний член).
Значит после переноса получаем:
.
Теперь работаем с числителем.
.
Значит
.
Осталось самое приятное: подставить наши результаты в дробь, и понять, что всё получилось
ч.т.д.
2)
Перемножим дробь "крест-накрест", получим:
по формуле разностти квадратов, получаем:
переносим в одну часть
,
что верно в силу основного тригонометрического тождества. Так как мы тождественными преобразованиями перешли от исходного выражения к тождественному равенству, значит изначально тоже было тождественное равенство, ч.т.д.
Пошаговое объяснение:
Для удобства набора решения, все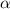 я заменил на
я заменил на
1)
Сначала предварительная подготовка:
То есть
Значит после переноса получаем:
Теперь работаем с числителем.
Значит
Осталось самое приятное: подставить наши результаты в дробь, и понять, что всё получилось
ч.т.д.
2)
Перемножим дробь "крест-накрест", получим:
по формуле разностти квадратов, получаем:
переносим в одну часть
что верно в силу основного тригонометрического тождества. Так как мы тождественными преобразованиями перешли от исходного выражения к тождественному равенству, значит изначально тоже было тождественное равенство, ч.т.д.
Пошаговое объяснение:
Для удобства набора решения, все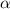 я заменил на
я заменил на
1)
Сначала предварительная подготовка:
То есть
Значит после переноса получаем:
Теперь работаем с числителем.
Значит
Осталось самое приятное: подставить наши результаты в дробь, и понять, что всё получилось
ч.т.д.
2)
Перемножим дробь "крест-накрест", получим:
по формуле разностти квадратов, получаем:
переносим в одну часть
что верно в силу основного тригонометрического тождества. Так как мы тождественными преобразованиями перешли от исходного выражения к тождественному равенству, значит изначально тоже было тождественное равенство, ч.т.д.