1. Запишите в виде выражения: частное от деления разности чисел 65 и 44 и 7.
Варианты ответов:
а) (65 – 44): 7
б) 65: ( 44 – 7)
в) (65 – 7): 44
г) 65 – 44 :7
2. Запишите в виде выражения: произведение суммы чисел 25 и 3 на 8.
Варианты ответов:
а) (25 +8)∙ 3
б) (25 + 3) ∙ 8
в) 25∙ (3+ 8)
г) 25 ∙ 3 +8
3. Найдите значение суммы у + х, если у= -5,8, а х = -3,6?
Варианты ответов:
а) 9,4
б) -9,4
в) -2,2
г) 2,2
4. Найдите значение разности х - у, если х= -2,8, а у = 4,6?
Варианты ответов:
а) 7,4
б) -7,4
в) -1,8
г) 1,8
5. Cравните значения выражений – 2х и 4х при х = -3.
Варианты ответов:
а) – 2х < 4х
б) – 2х > 4х
в) – 2х = 4х
г) – 2х ≥ 4х
6. Сравните значения выражений 3х и -5х при х = -2.
Варианты ответов:
а) 3х < -5х
б) 3х > -5х
в) 3х = -5х
г) 3х ≥ -5х
7.Составьте выражение по условию задачи: «Длина прямоугольника х см, а его
ширина на 10см больше. Найдите периметр прямоугольника».

Среди всех 3n учеников выберем такого ученика (точнее, одного из таких учеников), который имеет наибольшее число kk знакомых в одной из двух других школ. Пусть для определенности им оказался ученик А первой школы, который знает kk учеников, например, из второй школы. Тогда А знает n+1–kn+1–k учеников из третьей школы, причем n+1–k≥1n+1–k≥1, так как k≤nk≤n. Рассмотрим ученика В третьей школы, знакомого с А. Если В знает хотя бы одного ученика С из kk знакомых А во второй школе, то ученики A, В, С образуют искомую тройку. Если же В не знает никого из kk знакомых А во второй школе, то в этой школе он знаком не более чем с n–kn–k учениками, а значит, в первой школе он знаком не менее чем с n+1−(n−k)=k+1n+1−(n−k)=k+1 учениками, что противоречит выбору kk.

Переводим десятичные, смешанные дроби в неправильные и находим НОЗ:

1)

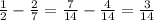
2)

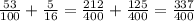
3)

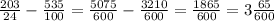
4)

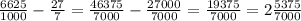
Объяснение:

Чтобы превратить десятичную дробь в неправильную, нужно смотреть на вид дроби (где запятая и какое число).

Например 5,35. После запятой - нули. То есть: 5,35*100 = 535/100. При делении неправильной дроби получается десятичная дробь.

Чтобы превратить смешанную дробь в неправильную, нужно целую часть умножить со знаменателем и сложить с числителем дроби.

Например 8 11/24. То что получилось - пишем в числитель, а знаменатель остаётся таким же. Значит: 8*24+11 = 203/24.