1) знайдіть область визначення функції що зображена на графіку 2) у який ще рік вироблялося стільки ж електроенергії, як у 1995?

1) знайдіть область визначення функції що зображена на графіку 2) у який ще рік вироблялося стільки

Показать ответ

Ответ:

ДавыдоваЮлия5678

15.07.2021 07:37

Пошаговое объяснение:

Номер 1. 90<α<180, cos(α)=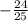 $-\frac{24}{25}$

Ограничения на угол α накладывают ограничения на sin(α): sin(α) >0 , т.к. угол находится во второй четверти.

$sin^2(\alpha )+cos^2(\alpha)=1\\sin(\alpha)=\sqrt{1-cos^2(\alpha)}\\ sin(\alpha)=\sqrt{1-\frac{24^2}{25^2} }=\frac{7}{25} \\ tg(\alpha)=\frac{sin(\alpha)}{cos(\alpha)} =-\frac{7}{24}\\ ctg(\alpha)=-\frac{24}{7}$

Номер 2.

а) cos(3π/5)*tg(π/9)

Сравним каждый множитель с 0:

tg(π/9)>0 т.к. sin(π/9)>0 и cos(π/9) >0, и если делить положительное число на положительное, то получится положительное

cos(3π/5) : 3π/5 - тупой угол => его косинус отрицательный

Мы умножаем положительное число на отрицательное и получаем отрицательное => cos(3π/5)*tg(π/9)<0

б)sin(4)cos(5)

Аналогично:

sin(4): π<4<2π=> sin(4)<0

cos(5): 3π/2<5<5π/2 =>cos(5)>0

sin(4)cos(5)<0

Номер 5.

$8sin^2(\alpha )-5cos^2(\alpha)=7\\cos^2(\alpha)=1-sin^2(\alpha)\\8sin^2(\alpha)-5(1-sin^2(\alpha))=7\\8sin^2(\alpha)-5+5sin^2(\alpha)=7\\13sin^2(\alpha)=12\\sin^2(\alpha)=\frac{12}{13}\\ cos^2(\alpha)=\frac{1}{13}\\ tg^2(\alpha)=\frac{sin^2(\alpha)}{cos^2(\alpha)}=12$

0,0(0 оценок)

Ответ:

Айнель2006

11.04.2021 15:13

Привет)

1. 9+5+2+3+0,5+2,5=23 ч - всего в распорядке дня.

2. 360°:23≈15,6° - 1 ч на круге

(0,5 ч =7,8°)

Теперь каждое значение (сон, школа и т.д.) умножаем на 15,6° и тем самым находим, сколько градусов будет на круговой диаграмме.

9•15,6=140,4° - сон

5•15.6=78° - школа

2•15.6=31,2° - д/з

3•15.6=46,8° - отдых

0.5•7.8=3.9° - работа с ПК

2.5•(7.8+15.6)°=58,5° - просмотр передач

Чтобы проверить, правильно ли вышло, мы должны сложить все значения и должно получиться 360°. У нас во втором действии приблизительно, поэтому будет не 360, а приблизительно.

140.4+78+31.2+46,8+3.9+58.5=358.8°