Рассмотрим обгон велосипеда быстрой машиной. Так как когда-нибудь таковой произойдёт, начнём считать всё с момента его свершения. Пусть скорость велосипеда ниже 27 км/ч, тогда, пока быстрая машина проезжает 5 сторон трассы (одну проезжает дважды), велосипед проезжает менее одной и обгон происходит не в вершине. Если скорость велосипеда больше 27 км/ч, но меньше 45 км/ч, то, пока быстрая машина проезжает 5 сторон, велосипед проезжает более одной стороны, но пока быстрая машина проезжает 6 сторон, велосипед проезжает менее двух сторон и обгон происходит не в вершине. Значит, скорость велосипеда равна 27 км/ч. Заметим, что пока велосипед проезжает одну сторону, быстрая машина проезжает 5 сторон и пока велосипед проезжает 6 сторон, медленная машина проезжает 10 сторон и оба обгона происходят в вершинах.
Пусть сторона квадрата равна a; В начальный момент времени все находятся в одной вершине квадрата.
Заметим, что скорость второй машины ровно в три раза превосходит скорость первой. Тогда первый обгон между двумя машинами случится тогда, когда первая проедет 2a (вторая проедет 3×2a=6a); Поэтому все обгоны между машинами будут в вершинах.
Пусть скорость велосипеда равна v; (i); Аналогично
(ii); (*); Также (**); Переставляя элементы в (i) получим равносильное утверждение: ;
Рассмотрим числа n и n+4: ; Рассмотрим все нечетные n; Тогда n и n+4 взаимно просты, а значит ; Получаем числа n∈{1,7,51}; Рассмотрим числа n такие, что
; Тогда ; Получаем числа n∈{6,18,106}; Осталось рассмотреть числа n, такие, что
; Отсюда ;
Тогда n∈{16,40,216}; Всего: n∈{1,6,7,16,18,40,51,106,216};
Рассмотрим обгон велосипеда быстрой машиной. Так как когда-нибудь таковой произойдёт, начнём считать всё с момента его свершения. Пусть скорость велосипеда ниже 27 км/ч, тогда, пока быстрая машина проезжает 5 сторон трассы (одну проезжает дважды), велосипед проезжает менее одной и обгон происходит не в вершине. Если скорость велосипеда больше 27 км/ч, но меньше 45 км/ч, то, пока быстрая машина проезжает 5 сторон, велосипед проезжает более одной стороны, но пока быстрая машина проезжает 6 сторон, велосипед проезжает менее двух сторон и обгон происходит не в вершине. Значит, скорость велосипеда равна 27 км/ч. Заметим, что пока велосипед проезжает одну сторону, быстрая машина проезжает 5 сторон и пока велосипед проезжает 6 сторон, медленная машина проезжает 10 сторон и оба обгона происходят в вершинах.
ответ: 27 км/ч.
Пусть сторона квадрата равна a; В начальный момент времени все находятся в одной вершине квадрата.
Заметим, что скорость второй машины ровно в три раза превосходит скорость первой. Тогда первый обгон между двумя машинами случится тогда, когда первая проедет 2a (вторая проедет 3×2a=6a); Поэтому все обгоны между машинами будут в вершинах.
Пусть скорость велосипеда равна v;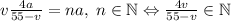
(i); Аналогично
Рассмотрим числа n и n+4: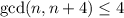
; Рассмотрим все нечетные n; Тогда n и n+4 взаимно просты, а значит 
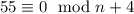; Получаем числа n∈{1,7,51}; Рассмотрим числа n такие, что
Тогда n∈{16,40,216}; Всего: n∈{1,6,7,16,18,40,51,106,216};
Условию (ii) удовлетворяет только число 33;
ответ: 33 км/ч