Дана функция у(х)=х²/(х²+2х+3). 1. Найти область определения функции. Функция дробная, знаменатель не может быть равен нулю. х²+2х+3 = 0. Квадратное уравнение, решаем относительно x: Ищем дискриминант: D=2^2-4*1*3=4-4*3=4-12=-8; Дискриминант меньше 0, уравнение не имеет корней. Значит, ограничений нет. 2. Исследовать функцию на чётность (нечётность) и на периодичность (для тригонометрических функций). f(-x) = (-x)² + 2*(-x) + 3 = x² - 2x + 3 ≠ f(x) и не равно -f(-x). Значит, функция не чётная и не нечётная. 3. Найти точки разрыва функции и вертикальные асимптоты (если они существуют). Точек разрыва и вертикальных асимптот нет. 4. Исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты; Наклонных асимптот нет, горизонтальная есть: у = 1 (решение в приложении). 5. Найти экстремумы и интервалы монотонности функции. Находим производную функции. y' = (2x(x+3))/((x²+2x+3)²) Приравниваем нулю (достаточно числитель). 2х(х+3) = 0. Имеем 2 критические точки: х = 0 и х = -3. Находим знаки производной в полученных промежутках. x = -4 -3 -2 0 1 y' = 8 0 -4 0 8. Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума. Функция: возрастает на промежутках х ∈ (-∞; -3)∪(0; +∞), убывает на промежутке х ∈ (-3; 0), максимум функции в точке х = -3, минимум х = 0. 6. Определить интервалы выпуклости и точки перегиба. Для этого находим вторую производную. y'' = (-4x³-18x²+18)/((x²+2x+3)³). Приравняв нулю числитель, находим 3 точки перегиба графика: х= -4,25098, х = -1,16089 и х = 0,911869. 7. Найти точки пересечения с осями координат, если возможно и некоторые дополнительные точки, уточняющие график. Ось Ох не пересекается, только есть точка касания х = 0. Ось Оу пересекается при х = 0. Дополнительные точки для построения графика даны в приложении.
ИССЛЕДОВАНИЕ 1. Область определения. Деление на ноль в знаменателе. Х≠ 1. Х∈(-∞;0)∪(0;+∞) 2. Вертикальная асимптота: Х= 1. 3. Пересечение с осью Х. Y(x) = 0 - нет. 4. Пересечение с осью У - нет 5. Наклонная асимптота k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность. Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x) Функция ни четная ни нечетная. 7. Поведение в точке разрыва. lim(->0-) Y(x) = -∞. lim(->0+) Y(x) = +∞ 8, Первая производная. 6. Локальные экстремумы. Y'(x) = 0, x1 = - 3/2, x2 = 3/2 Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12. 7. Участки монотонности функции. Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2] 8. Вторая производная.
Корней нет. Точек перегиба (на графике) - нет. 9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
1. Найти область определения функции.
Функция дробная, знаменатель не может быть равен нулю.
х²+2х+3 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=2^2-4*1*3=4-4*3=4-12=-8; Дискриминант меньше 0, уравнение не имеет корней.
Значит, ограничений нет.
2. Исследовать функцию на чётность (нечётность) и на периодичность (для тригонометрических функций).
f(-x) = (-x)² + 2*(-x) + 3 = x² - 2x + 3 ≠ f(x) и не равно -f(-x).
Значит, функция не чётная и не нечётная.
3. Найти точки разрыва функции и вертикальные асимптоты (если они существуют).
Точек разрыва и вертикальных асимптот нет.
4. Исследовать поведение функции в бесконечности, найти горизонтальные и наклонные асимптоты;
Наклонных асимптот нет, горизонтальная есть: у = 1 (решение в приложении).
5. Найти экстремумы и интервалы монотонности функции.
Находим производную функции.
y' = (2x(x+3))/((x²+2x+3)²)
Приравниваем нулю (достаточно числитель).
2х(х+3) = 0.
Имеем 2 критические точки: х = 0 и х = -3.
Находим знаки производной в полученных промежутках.
x = -4 -3 -2 0 1
y' = 8 0 -4 0 8.
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
Функция: возрастает на промежутках х ∈ (-∞; -3)∪(0; +∞),
убывает на промежутке х ∈ (-3; 0),
максимум функции в точке х = -3,
минимум х = 0.
6. Определить интервалы выпуклости и точки перегиба.
Для этого находим вторую производную.
y'' = (-4x³-18x²+18)/((x²+2x+3)³).
Приравняв нулю числитель, находим 3 точки перегиба графика:
х= -4,25098, х = -1,16089 и х = 0,911869.
7. Найти точки пересечения с осями координат, если возможно и некоторые дополнительные точки, уточняющие график.
Ось Ох не пересекается, только есть точка касания х = 0.
Ось Оу пересекается при х = 0.
Дополнительные точки для построения графика даны в приложении.
ДАНО
Y = (x² + 9)/x
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ 1.
Х∈(-∞;0)∪(0;+∞)
2. Вертикальная асимптота: Х= 1.
3. Пересечение с осью Х. Y(x) = 0 - нет.
4. Пересечение с осью У - нет
5. Наклонная асимптота
k = lim(+∞)Y(x)/x = 4*x/x = 4. Уравнение асимптоты: Y = 4*x.
6. Проверка на чётность.
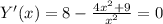
Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)
Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->0-) Y(x) = -∞.
lim(->0+) Y(x) = +∞
8, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0, x1 = - 3/2, x2 = 3/2
Максимум Y(-3/2)= .-12.
Минимум Y(3/2) = 12.
7. Участки монотонности функции.
Возрастает - Х∈(-∞;-3/2]∪[3/2;+∞).
Убывает - Х∈[-3/2;0)∪(0;3/2]
8. Вторая производная.
Корней нет. Точек перегиба (на графике) - нет.
9. Выпуклая - "горка" - Х∈(-∞;0). Вогнутая - "ложка" - Х∈(0;+∞)
10. График в приложении