пусть х м - длина основания равнобедренного треугольника, где x> 0, тогда длина боковой стороны этого же равнобедренного треугольника по условию равна 12х м, т.к. периметр этого треугольника равен 10 м по условию, получаем уравнение:
х+12х+12х=10
25х=10
х=0,4
значит, 0,4 м - длина основания.
ответ: 0,4 м.
теорема пифагора: , где с - гипотенуза, а а и b - катеты прямоугольного треугольника.
к равнобедренному треугольнику она не относится (исключение составляет если основание равнобедренного треугольника является гипотенузой прямоугольного треугольника, т.е. угол, лежащий против основания равнобедренного треугольника - прямой, т.е. равен ).
Для начала заметим, что если x в левой стороне под корнем заменить подобным же выражением, повторяя и повторяя операцию (то есть положить ), то получим верное равенство (конечно, нужно доказать, что ряд сходится, но этого сейчас не требуется, предположим, что это правда).
Получили задачу о нахождении числа ;
Пусть ; Тогда получим систему: ; Сделаем переход: ; Осталось решить уравнение: ; Сделав отбор корней, получим: ; Вспомним теперь, что , откуда и следует ответ А). Но для полноты давайте докажем этот факт.
Пусть ; Тогда ; Заметим, что ; Иными словами , опять же сделав отбор корней, приходим к требуемому
пусть х м - длина основания равнобедренного треугольника, где x> 0, тогда длина боковой стороны этого же равнобедренного треугольника по условию равна 12х м, т.к. периметр этого треугольника равен 10 м по условию, получаем уравнение:
х+12х+12х=10
25х=10
х=0,4
значит, 0,4 м - длина основания.
ответ: 0,4 м.
теорема пифагора: , где с - гипотенуза, а а и b - катеты прямоугольного треугольника.
к равнобедренному треугольнику она не относится (исключение составляет если основание равнобедренного треугольника является гипотенузой прямоугольного треугольника, т.е. угол, лежащий против основания равнобедренного треугольника - прямой, т.е. равен ).
Для начала заметим, что если x в левой стороне под корнем заменить подобным же выражением, повторяя и повторяя операцию (то есть положить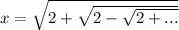
), то получим верное равенство (конечно, нужно доказать, что ряд сходится, но этого сейчас не требуется, предположим, что это правда).
Получили задачу о нахождении числа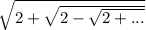
;
Пусть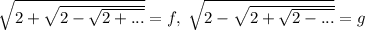
; Тогда получим систему: 
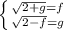; Сделаем переход: 
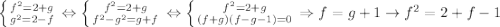; Осталось решить уравнение: 
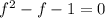; Сделав отбор корней, получим: 
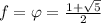; Вспомним теперь, что 
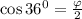, откуда и следует ответ А). Но для полноты давайте докажем этот факт.
Пусть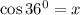
; Тогда 
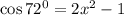; Заметим, что 
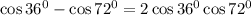; Иными словами 
, опять же сделав отбор корней, приходим к требуемому