1. Из граничных точек точка -3 отмечена окружностью, поэтому не принадлежит ко множеству, точка 8 отмечен кругом, поэтому принадлежит ко множеству. Если граничное значение не принадлежит ко множеству, то в числовом интервале используется круглая скобка, а если граничное значение принадлежит ко множеству, то в числовом интервале используется квадратная скобка. Поэтому б) (-3; 8]
2. Дано х ≤ -5, что означает все точки множества меньше либо равно -5 (то есть лежат слева от -5) и множество снизу не ограничено. Поэтому ответ а) подходит.
3.
Тогда имеет место двойное неравенство: -1≤ х < 2. ответ: [-1; 2)
4.
Отсюда x>-3 или x∈ (-3; +∞)
5. -6 ≤ 6-2x < 9
-6-6 ≤ -2x < 9-6
-12 ≤ -2x < 3
-12:(-2) ≥ x > 3:(-2)
-1,5 < x ≤ 6 или x∈ (-1,5; 6]
6. При каких значениях переменной имеет смысл выражение
Данное выражение имеет смысл, если подкоренные выражения не отрицательные:
Кратные 6 --(24;12;6;) Кратное числу, это число которое делится на данное число умножаем подряд на 1,2,3.. Само число и ответ это кратное числу. 6•1=6; 6•2=12; 6•3=18; 6•4=24 ; дальше не подходят (6•5=30 больше чем 24).
6;12;18;24 кратны 6; но мы выбираем те, что будут делателями 24, 24:18 =не делится нацело, не подходит.
Совпадают 6;12;24.
ответ: Делителем 24 и кратным 6 являются числа 6; 12; 24.
1. б) (-3; 8]
2. а)
3. x∈ [-1; 2)
4. x∈ (-3; +∞)
5. x∈ (-1,5; 6]
6. x∈ [1/5; 2]
7. x∈ (-∞; 12]
8. x∈ [-2; 3]
Пошаговое объяснение:
1. Из граничных точек точка -3 отмечена окружностью, поэтому не принадлежит ко множеству, точка 8 отмечен кругом, поэтому принадлежит ко множеству. Если граничное значение не принадлежит ко множеству, то в числовом интервале используется круглая скобка, а если граничное значение принадлежит ко множеству, то в числовом интервале используется квадратная скобка. Поэтому б) (-3; 8]
2. Дано х ≤ -5, что означает все точки множества меньше либо равно -5 (то есть лежат слева от -5) и множество снизу не ограничено. Поэтому ответ а) подходит.
3.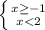
Тогда имеет место двойное неравенство: -1≤ х < 2. ответ: [-1; 2)
4.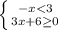
Отсюда x>-3 или x∈ (-3; +∞)
5. -6 ≤ 6-2x < 9
-6-6 ≤ -2x < 9-6
-12 ≤ -2x < 3
-12:(-2) ≥ x > 3:(-2)
-1,5 < x ≤ 6 или x∈ (-1,5; 6]
6. При каких значениях переменной имеет смысл выражение
Данное выражение имеет смысл, если подкоренные выражения не отрицательные:
1/5 ≤ x ≤ 2 или x∈ [1/5; 2]
7. Решите совокупность неравенств
Отсюда х ≤ 12 или x∈ (-∞; 12]
8.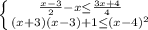
Отсюда -2 ≤ х ≤ 3 или x∈ [-2; 3]
24и кратным 6,
Делитель это число на которое делится данное число.
24:2=12; 24:12=2. и 2 и 12 делители просто делим от 1 до самого числа на все что делится
24:1=24; 24:2=12; 24:3=8; 24:4=6; 24:6= 4; 24:8=3; 24:12=2; 24:24=1.
Делители 24-- (1;2;3;4;6;8;12;24)
Кратные 6 --(24;12;6;)
Кратное числу, это число которое делится на данное число умножаем подряд на 1,2,3.. Само число и ответ это кратное числу.
6•1=6; 6•2=12; 6•3=18; 6•4=24 ; дальше не подходят (6•5=30 больше чем 24).
6;12;18;24 кратны 6; но мы выбираем те, что будут делателями 24,
24:18 =не делится нацело, не подходит.
Совпадают 6;12;24.
ответ:
Делителем 24 и кратным 6 являются числа 6; 12; 24.
36 и кратным 9,
36:1=36; 36:2=18; 36:3=12; 36:4=9; 36:6=6; 36:9=4; 36:12=3; 36:18=2; 36:36=1;
делители 36 (1;2; 3;4;6;9;12;18;36).
Кратны 9.
9•1=9; 9•2=18; 9•3=27; 9•4=36.
Совпадают 9;18;36.
ответ: делителем 36 и кратными 9 являются числа 9;18;36.
100 и кратным 20,
100:1=100; 100:2=50; 100:4=25; 100:5=20; 100:10=10; 100:20=5; 100:25=4; 100:50=2; 100:100=1.
Делители 100 (1;2;4;5;10;20;25;50;100).
Кратные 20.
20•1=20; 20•2=40; 20•3=60; 20•4=80; 20•5=100.
Совпадают 20;100.
ответ: делителем 100 и кратные 20 являются сами числа 20 и 100.
108 и кратным 36
108:1=108; 108:2=54; 108:3=36; 108:4=27; 108:6=18; 108:9=12; 108:12=9; 108:18=6; 108:36=3; 108:54=2; 108:108=1
Делители 108 (1;2;3;4;6;9;12;18;36;54;108)
Кратные 36.
1•36=36; 2•36=72; 3•36=108.
Совпадают (36;108)
ответ: делителем 108 и кратными 36 являются сами числа 36 и 108.