Построим равнобедренную трапецию ABCD с высотой CF (см. Рис. 1).
Согласно условию: AD=18 см, BC=10 см, CF=3 см. Для дальнейших вычислений нам понадобится длина боковой стороны трапеции AB=CD.
Т.к. трапеция равнобедренная, то FD = (AD-BC):2 = 4 см.
ΔCDF - прямоугольный с катетами CF=3 см, FD=4 см, значит он египетский, и его гипотенуза CD=5 см.
При вращении такой трапеции вокруг короткого основания образуется цилиндр с равными осевыми конусообразными выемками с обеих сторон (См. рис. 1.2, 2.1, 2.2). Радиус такого цилиндра равен высоте трапеции R=CF=3 см, а высота цилиндра равна длинному основанию трапеции H=AD=18 см.
Образующей конуса-выемки является боковая сторона трапеции L=CD=5 см, радиус равен радиусу цилиндра R=3 см.
Искомая площадь полной поверхности фигуры вращения состоит из площади боковой поверхности цилиндра и двух боковых поверхностей конусов-выемок.
138π см²
Пошаговое объяснение:
Построим равнобедренную трапецию ABCD с высотой CF (см. Рис. 1).
Согласно условию: AD=18 см, BC=10 см, CF=3 см. Для дальнейших вычислений нам понадобится длина боковой стороны трапеции AB=CD.
Т.к. трапеция равнобедренная, то FD = (AD-BC):2 = 4 см.
ΔCDF - прямоугольный с катетами CF=3 см, FD=4 см, значит он египетский, и его гипотенуза CD=5 см.
При вращении такой трапеции вокруг короткого основания образуется цилиндр с равными осевыми конусообразными выемками с обеих сторон (См. рис. 1.2, 2.1, 2.2). Радиус такого цилиндра равен высоте трапеции R=CF=3 см, а высота цилиндра равна длинному основанию трапеции H=AD=18 см.
Образующей конуса-выемки является боковая сторона трапеции L=CD=5 см, радиус равен радиусу цилиндра R=3 см.
Искомая площадь полной поверхности фигуры вращения состоит из площади боковой поверхности цилиндра и двух боковых поверхностей конусов-выемок.
Площадь боковой поверхности цилиндра: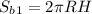 .
.
Площадь боковой поверхности конуса-выемки: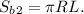
Площадь полной поверхности: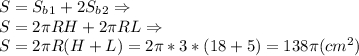
4 км/ч скорость пешехода , 16 км/ч скорость велосипедиста.
Пошаговое объяснение:
Скорость пешехода - х км/ч
Скорость велосипедиста - у км/ч
1 часть задачи:
Пешеход:
Время в пути t₁= (10+30) мин = 40 мин = 40/60 ч. = 2/3 ч.
Расстояние S₁ = 2/3 *х км
Велосипедист :
Время в пути t₂ = 10 мин.= 1/6 часа
Расстояние S₂= 1/6 * у
S₁= S₂ ⇒ первое уравнение : 2/3 * х = 1/6 *у
2 часть задачи:
Пешеход:
t₃= 3 часа
S₃= 3 x км
Велосипедист:
t₄= 1/2 ч.
S₄= 1/2 * у км
S₄ - S₃ = 4 км ⇒ второе уравнение :3х - 1/2 у = 4
Система уравнений
{2/3 x = 1/6 y |*6
{3x - 1/2 y= 4 |*2
{4x = y ⇒ y =4x
{6x - y =8
Метод подстановки
6х-4х =8
2х=8
х=8/2
х= 4 (км/ч) скорость пешехода
у=4*4 = 16 (км/ч) скорость велосипедиста
Подробнее - на -