1386. мотоциклист выехал из дома и через некоторое
время вернулся назад. На рисунке 202 изображен
изменения расстояния мотоциклиста от дома в
зависимости от времени (график движения
мотоциклиста).
1) Какое расстояние проехал мотоциклист за первый час
движения?
2) На каком расстоянии от дома мотоциклист остановился
для первого отдыха? для второго отдыха?
3) Сколько длился первый отдых? второй отдых?
4) На каком расстоянии от дома был мотоциклист через
5ч после начала движения?
5) С какой скоростью двигался ,
полчаса?
НЕ
| 20.ответить на ва
Для начала надо узнать сумму чисел от 1 до 10:
1+2+3...+8+9+10=55.
Теперь давайте думать логически:"В нашем пятиугольнике каждая последняя цифра должна быть началом следующей комбинации".
Чтобы легко справится с этим заданием, надо начинать с самого крупного числа и к нему добавлять более мелкие цифры, но у пятиугольника 5 сторон, а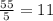
, но так как 5 чисел связны с двумя сторонами, то сумма стороны будет не 11, а 16. Теперь мы знаем, сколько должна давать каждая сторона и мы можем приступать к работе:
10+2+4; 4+9+3; 3+6+7; 7+8+1; 1+5+10.
Вот и всё! Теперь просто запишите числа в такой последовательности (10, 2, 4, 9, 3, 6, 7, 8, 1, 5) по часовой стрелке.
А) a : b: c = 3 : 6 : 8;
B) a : b: c = 18 : 15 : 20
Пошаговое объяснение:
А) Рассмотрим a : b = 1 : 2 в частях.
Это отношение 1-ой части a к 2-ум частям b.
Рассмотрим b : c = 3 : 4 в частях.
Это отношение 3-х частей b к 4-ём частям c.
Выразим данные отношения так, чтобы количество частей b было одинаковым.
НОК (2; 3) = 3 · 2 = 6
Получаем:
a : b = 1 : 2 = 3 : 6;
b : c = 3 : 4 = 6 : 8; => a : b: c = 3 : 6 : 8.
В) Рассмотрим a : b = 3 : 2,5 в целых частях.
a : b = 6 : 5
Это отношение 6-ти частей a к 5-ти частям b.
Рассмотрим b : c = 1,2 : 2,5 в целых частях.
b : c = 12 : 25
Это отношение 12-ти частей b к 25-ти частям c.
Выразим данные отношения так, чтобы количество частей b было одинаковым.
НОК (5; 12) = 2 · 2 · 3 · 5 = 60
Получаем:
a : b = 3 : 2,5 = 72 : 60;
b : c = 3 : 4 = 60 : 80; => a : b: c = 72 : 60 : 80 = 18 : 15 : 20.