( 16 - 81/3 ) : ( -25/9 )

Итальянские исследователи из института кристаллографии в бари, ведомые профессором джулио фанти из университета падуи, применили самое современное оборудование для того, что рассмотреть в мельчайших — нано - подробностях волокна туринской плащаницы. просвечивающий электронный микроскоп и широкоугольный рентгеновский сканирующий микроскоп, которыми они обзавелись, позволили увидеть то, что раньше ускользало из поля зрения предшественников. итальянцы полагают, что обнаружили на ткани частицы крови — настоящей человеческой крови. а в них - ферритин — биологическое вещество на основе железа и креатинин — аминокислотный комплекс, который поступает в кровь из мышц. эти вещества присутствовали в таком характерном виде, позволившим сделать вывод: кровь принадлежит человеку, которого нещадно мучили — пытали и не давали пить.

7

Пошаговое объяснение:

Вспомним признак делимости на 9: число делится на 9 тогда и только тогда, когда его сумма цифр делится на 9.

Этот признак работает и для равноостаточности при делении на 9. То есть, число и его сумма цифр имеют одинаковый остаток при делении на 9.

Пусть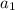 - изначальное число и 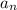- сумма цифр числа 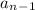. Пусть остаток при делении на 9 у числа 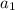- r, тогда и у числа 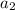остаток при делении на 9 тоже r. Но тогда и у чисел 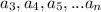остаток при делении на 9 равен r. Но так как r - чисто от 0 до 9, то это и есть наша оставшаяся в конце цифра.

Тогда нам нужно всего лишь найти остаток при делении на 9 у числа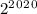  . А он такой же, как у числа 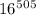, и такой же, как у числа 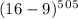, и такой же, как у числа 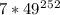, а он такой же, как у числа 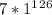, а это равно 7.