Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два решения .
P.S. Легко подобрать корни по теореме Виета , например, для такого уравнения .
4) Графический решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения : .
1) Решение через дискриминант .
2) Решение с выделения полного квадрата .
3) Решение с теоремы Виета.
Второе уравнение фактически получили такое же, как и было задано . Подобрать корни без решения уравнения через дискриминант в этом случае сложно . Поэтому реально работают первые два решения .
P.S. Легко подобрать корни по теореме Виета , например, для такого уравнения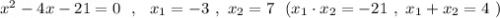 .
.
4) Графический решения уравнения . Построить параболу и найти точки пересечения с осью ОХ . Но в данном случае точные значения найти практически невозможно. Только приближённые значения :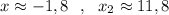 .
.
32.4
1) P=a+b+c; P=10+8+12=30(см.)
P=30см.
2) a=P-b-c
a=60-14,2-23=22,8(м.)
a=22,8м.
3) b=P-a-c
1м=100см
b=100-37-37=26(см.)
b=26см.
4) У равностороннего треугольника все стороны равны, значит a=b=c
a=b=c=P/3
1,2см=12мм
a=b=c=12/3=4(мм.)
a=b=c=4мм.
32.6
Вычислим периметр треугольника с катетами 3см, 4см.
Периметр треугольника равен сумме всех его сторон.
Так как треугольник прямоугольный, а катеты нам известны, найдём гипотенузу по теореме Пифагора:
x²=3²+4²
x=√3²+4²
x=√9+16
x=√25
x=5
Значит гипотенуза равна 5 см.
Находим периметр:
P=3+4+5=12см.
ответ: 12см.