Доказать, что наименьшее натуральное число , для которого , должно быть делителем ; - простое число, не делящее целого числа .
Пошаговое объяснение:
Пусть число найдено.
Пусть - остаток от деления на , т.е.
Согласно теореме Ферма .
Но . Значит,
.
При этом, по построению, , откуда, если натуральное, получаем противоречие с тем, что - минимальное из чисел, удовлетворяющих условию. Значит, [учитывая, что из теоремы Ферма следует существование искомого числа] - а это и означает, что - делитель числа .
Оба двухзначных числа оканчиваются на одну и ту же цифру (пересказал условие, хех). Произведение двух таких чисел может оканчиваться на 1, если они оканчиваются либо на 1, либо на 9.
Разложим число 2001 на множители. Сразу бросается в глаза, что оно делится на 3:
Разложим 667 на множители. Тут я считерю и воспользуюсь калькулятором, получается 23*29 — это простые числа. Я не знаю, как факторизовать их без калькулятора, кроме метода перебора.
То есть . Есть два варианта сделать два двухзначных числа:
— последние цифры одинаковы, подходит.
— последние цифры одинаковы, не подходит.
ответ: .
P. S. Возможно, перейдя к десятичному представлению чисел и найдя там какие-то закономерности, можно решить проще без калькулятора. Попробуйте:
Условие:
Доказать, что наименьшее натуральное число
, для которого 
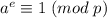, должно быть делителем 
; 
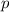- простое число, не делящее целого числа 
.
Пошаговое объяснение:
Пусть число
найдено.
Пусть
- остаток от деления 
на 
, т.е.
Согласно теореме Ферма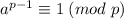
.
Но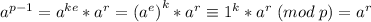
. Значит,
При этом, по построению,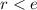
, откуда, если 
натуральное, получаем противоречие с тем, что 
- минимальное из чисел, удовлетворяющих условию. Значит, [учитывая, что из теоремы Ферма следует существование искомого числа]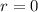 
- а это и означает, что 
- делитель числа 
.
Ч.т.д.
Оба двухзначных числа оканчиваются на одну и ту же цифру (пересказал условие, хех). Произведение двух таких чисел может оканчиваться на 1, если они оканчиваются либо на 1, либо на 9.
Разложим число 2001 на множители. Сразу бросается в глаза, что оно делится на 3:
Разложим 667 на множители. Тут я считерю и воспользуюсь калькулятором, получается 23*29 — это простые числа. Я не знаю, как факторизовать их без калькулятора, кроме метода перебора.
То есть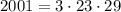
. Есть два варианта сделать два двухзначных числа:
ответ:
.
P. S. Возможно, перейдя к десятичному представлению чисел и найдя там какие-то закономерности, можно решить проще без калькулятора. Попробуйте: