1. Область определения x ∈(-∞,+∞), функция - чётная
2. y' = -x³+2x
3. y'=0, 2x-x³=0, x(2-x²)=0, стационарные точки x=0, x=±
4. y'>0, x>0, x<, x∈(0,
y'>0, x<0, x< -, x∈(-∞,-
Тогда промежуток возрастания x ∈(-∞,-)∪(0,
Промежуток убывания x ∈ (-,0)∪(
В точке x = 0, производная меняет знак с минуса на плюс, то есть x=0 - точка минимума
в окрестности точек x=± производная меняет знак с плюса на минус, это точки максимума
y(0)=0
y(±)=2-1=1
вот и график, построенный в Октаве
Пошаговое объяснение:
1) (-Б;+Б)
2)y'=-x^3+2x=-x(x^2-2), y'=0, -x(x^2-2)=0, x=0, x^2=2, x=-V2,
x=V2 (V2 - корень из 2), 3) три точки: -V2, 0, V2
4)___+__[-V2]___-___[0]___+___[V2]___-___ y'
возр. max убыв. min возр. max убыв у
5) y(-V2)=- 1/4*(-V2)^4+(-V2)^2=-1+2= 1
y(V2)=1
6) НА оси ОХ отметить точки -V2=~-1,4, 0 и V2=~1,4 и
отметить значения функции в этих точках, функция четная,
симметрично оси ОУ , можно взять дополнит. точки х=+-2
и найти значения функции в этих точках
1. Область определения x ∈(-∞,+∞), функция - чётная
2. y' = -x³+2x
3. y'=0, 2x-x³=0, x(2-x²)=0, стационарные точки x=0, x=±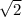
4. y'>0, x>0, x<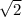
, x∈(0,
y'>0, x<0, x< -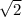
, x∈(-∞,-
Тогда промежуток возрастания x ∈(-∞,-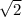
)∪(0,
Промежуток убывания x ∈ (-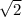
,0)∪(
В точке x = 0, производная меняет знак с минуса на плюс, то есть x=0 - точка минимума
в окрестности точек x=±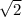
производная меняет знак с плюса на минус, это точки максимума
y(0)=0
y(±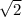
)=2-1=1
вот и график, построенный в Октаве
Пошаговое объяснение:
Пошаговое объяснение:
1) (-Б;+Б)
2)y'=-x^3+2x=-x(x^2-2), y'=0, -x(x^2-2)=0, x=0, x^2=2, x=-V2,
x=V2 (V2 - корень из 2), 3) три точки: -V2, 0, V2
4)___+__[-V2]___-___[0]___+___[V2]___-___ y'
возр. max убыв. min возр. max убыв у
5) y(-V2)=- 1/4*(-V2)^4+(-V2)^2=-1+2= 1
y(V2)=1
y(0)=0
6) НА оси ОХ отметить точки -V2=~-1,4, 0 и V2=~1,4 и
отметить значения функции в этих точках, функция четная,
симметрично оси ОУ , можно взять дополнит. точки х=+-2
и найти значения функции в этих точках