2.2. фигура составлена из двух равных плос- ких углов с общей вершиной. сколько всего раз- личных осей симметрии может иметь эта фигура? 1) ни одной; 2) одну; 3) две; 4) бесконечное много.
Сумма всех чисел на доске равна то есть нечетна. Покажем, что четность суммы не меняется, то есть последнее число должно оказаться нечетным.
База: первым ходом стираются два числа. Так как их разность той же четности, что и их сумма, то четность суммы чисел не изменилась.
Переход: пусть после k ходов сумма нечетна. Покажем что следующим ходом мы не поменяем четность сумма. Но для этого достаточно применить рассуждения изложенные в базе. Значит через k+1 ход сумма чисел останется нечетной.
Так как 0 - число четное, а в итоге должно получиться нечетное число, то ответ на задачу отрицателен.
729 914,6419
- 118
81
- 376
324
-520
486
-340
324
- 160
81
- 790
729
61
ответ:914,6419=914,642 остаток 61
- 50381 |___76__
456 662,9078
- 478
456
-221
152
-690
684
- 600
532
- 680
608
72
ответ:662,9078=662,908 остаток 72
Сумма всех чисел на доске равна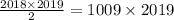
то есть нечетна. Покажем, что четность суммы не меняется, то есть последнее число должно оказаться нечетным.
База: первым ходом стираются два числа. Так как их разность той же четности, что и их сумма, то четность суммы чисел не изменилась.
Переход: пусть после k ходов сумма нечетна. Покажем что следующим ходом мы не поменяем четность сумма. Но для этого достаточно применить рассуждения изложенные в базе. Значит через k+1 ход сумма чисел останется нечетной.
Так как 0 - число четное, а в итоге должно получиться нечетное число, то ответ на задачу отрицателен.
ответ: нет