ну типо так?!
Пошаговое объяснение:
||2x – 4| – 5| = 9|+7| = 7
|-7| = 7,
поэтому, если |x| = 7, то делаем вывод, что x = +-7
A) |2x-5|-1 = 7 или |2x-5|-1 = -7
|2x-5| = 8 или |2x-5| = -6 ---это невозможно по определению модуля
2x-5 = 8 или 2x-5 = -8
2x = 13 или 2x = -3
x = 6.5 или x = -1.5
Б) |2x-1|-5 = 7 или |2x-1|-5 = -7
|2x-1| = 12 или |2x-1| = -2 ---это невозможно по определению модуля
2x-1 = 12 или 2x-1 = -12
2x = 13 или 2x = -11
x = 6.5 или x = -5.5
3x+2 = 5x+6 или 3x+2 = -(5x+6)
2x = -4 или 8x = -8
x = -2 или x = -1
4) члены геометрической прогрессии
b₁=3к-2
b₂=2к
b₃=к+3
а)
мы знаем, что отношение , составим такие отношения
⇒ 4k² = (3k-1)(k+3) ⇒ k²-7k+6 =0 ⇒ k₁ = 1; k₂ = 6
b) теперь строим прогрессии
для k₁ = 1 : b₁=3*1-2=1; b₂=2*1=2; b₃=1+3= 4 это возрастающая прогресстя
для k₂ = 6 b₁=3*6-2=16; b₂=2*6=12; b₃=6+3= 9 - это бесконечно убывающая геометрическая прогрессия, ее сумма
, у нас b₁= 16, найдем q= b₂/b₁= 12/16= 0.75, тогда
5.
рассуждаем так, в каждом последующем ряду бревен будет на 1 меньше, тогда n-член арифметической прогрессии имеет вид
, посмотрим, какой ряд будет последним (будет иметь одно бревно)
12-(n-1)=1 ⇒ n=12
найдем сумму 12 членов арифметической прогрессии
ну типо так?!
Пошаговое объяснение:
||2x – 4| – 5| = 9|+7| = 7
|-7| = 7,
поэтому, если |x| = 7, то делаем вывод, что x = +-7
A) |2x-5|-1 = 7 или |2x-5|-1 = -7
|2x-5| = 8 или |2x-5| = -6 ---это невозможно по определению модуля
2x-5 = 8 или 2x-5 = -8
2x = 13 или 2x = -3
x = 6.5 или x = -1.5
Б) |2x-1|-5 = 7 или |2x-1|-5 = -7
|2x-1| = 12 или |2x-1| = -2 ---это невозможно по определению модуля
2x-1 = 12 или 2x-1 = -12
2x = 13 или 2x = -11
x = 6.5 или x = -5.5
3x+2 = 5x+6 или 3x+2 = -(5x+6)
2x = -4 или 8x = -8
x = -2 или x = -1
Пошаговое объяснение:
4) члены геометрической прогрессии
b₁=3к-2
b₂=2к
b₃=к+3
а)
мы знаем, что отношение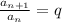 , составим такие отношения
, составим такие отношения
b) теперь строим прогрессии
для k₁ = 1 : b₁=3*1-2=1; b₂=2*1=2; b₃=1+3= 4 это возрастающая прогресстя
для k₂ = 6 b₁=3*6-2=16; b₂=2*6=12; b₃=6+3= 9 - это бесконечно убывающая геометрическая прогрессия, ее сумма
5.
рассуждаем так, в каждом последующем ряду бревен будет на 1 меньше, тогда n-член арифметической прогрессии имеет вид
12-(n-1)=1 ⇒ n=12
найдем сумму 12 членов арифметической прогрессии