2. а) постройте график и запишите формулу прямойпропорциональности, проходящий через точку а(-4; 12).3. постройте график функции и исследуйте его если можно| а) х=3 (0,5] 6) y=-2 [0,5] в) 2x-y-6=0 [2]
Проверим это правило посчитав определитель второй степени:
Поменяем столбцы местами:
Если брать некоторые абстрактные значения:
Пусть
Поменяем столбцы местами:
Далее можно было бы рассмотреть определитель n*n, но мне кажется, что и эта демонастрация будет весомым подкреплением моего заверения: что при перестановке столбцов знак определителя меняется на противоположный.
Во-первых, очень часто в системе уравнений вообще невозможно посчитать определитель, так как матрица отвечающая системе оказывается не квадратной.
А во-вторых, разумеется, определитель системы поменяет знак, если системе будет отвечать квадратная матрица и вы переставите столбцы.
Главное не путать матрицу элементов и определитель этой матрицы, это разные сущности!
Когда вы переставляете столбцы - вы меняете определитель, а система остается эквивалентной (когда перестановка осуществляется в пределах левой части, или в пределах правой. При переносе столбцов из левой в праву, или из правой в левую, надо домножать столбец на -1).
Общим знаменателем является 12
3*3/12 и 1*2/12
9/12 и 2/12
5/6 и 7/8
Общим знаменателем является 24
5*4/24 и 7*3/24
20/24 и 21/24
9/10 и 1/4
Общим знаменателем является 20
9*2/20 и 1*5/20
18/20 и 5/20
2/15 и 1/6
Общим знаменателем является 30
2*2/30 и 1*5/30
4/30 и 5/30
11/12 и 3/8
Общим знаменателем является 24
11*2/24 и 3*3/24
22/24 и 9/24
1/16 и 5/12
Общим знаменателем является 48
1*3/48 и 5*4/48
3/48 и 20/48
13/18 и 1/10
Общим знаменателем является 90
13*5/90 и 1*9/90
65/90 и 9/90
5/24 и 15/16
Общим знаменателем является 48
5*2/48 и 15*3 /48
10/48 и 45/48
Проверим это правило посчитав определитель второй степени:
Поменяем столбцы местами:
Если брать некоторые абстрактные значения:
Пусть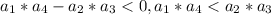
Поменяем столбцы местами:
Далее можно было бы рассмотреть определитель n*n, но мне кажется, что и эта демонастрация будет весомым подкреплением моего заверения: что при перестановке столбцов знак определителя меняется на противоположный.
Во-первых, очень часто в системе уравнений вообще невозможно посчитать определитель, так как матрица отвечающая системе оказывается не квадратной.
А во-вторых, разумеется, определитель системы поменяет знак, если системе будет отвечать квадратная матрица и вы переставите столбцы.
Главное не путать матрицу элементов и определитель этой матрицы, это разные сущности!
Когда вы переставляете столбцы - вы меняете определитель, а система остается эквивалентной (когда перестановка осуществляется в пределах левой части, или в пределах правой. При переносе столбцов из левой в праву, или из правой в левую, надо домножать столбец на -1).