2. Из бочки израсходовали 84 литра бензина, что составляет 2/3 всего имеющегося там бензина. Сколько бензина было в бочке?

Показать ответ

Ответ:

КапитанПрайс3000

15.06.2022 13:34

Пошаговое объяснение:

1) 20,8

3) 0,00241‬

5) 2,15

2) 322291

4) 0,025

6) 4

200-1,05+2,62=201,57

y-12,8=0,25

y=13,05

Дано:

S=156,3 км

t(встречи)=3 часа

v(груз.)=65,4 км/час

Найти:

v(велос.)=? км/час

Решение

1) Посчитаем какое расстояние проехал грузовик до встречи с велосипедистом, зная что он ехал 3 часа со скоростью 65,4 км/час:

S(груз.)=v(скорость)×t(время)=65,4×3=196,2 (км)

2) Посчитаем какое расстояние проехал велосипедист за 3 часа, зная что грузовик его догнал через 196,2 км, проехав дополнительно 156,3 км (расстояние между сёлами):

196,2-156,3=39,9 (км)

3) Велосипедист проехал 39,9 км за 3 часа, тогда его скорость равна:

v(велос.)=S÷t=39,9÷3=13,3 (км/час)

ответ: скорость велосипедиста равна 13,3 км/час.

0,0(0 оценок)

Ответ:

lidiyamartin9

21.03.2023 21:39

ответ: (e-1)/3

Пошаговое объяснение:

Найдём неопределённый интеграл функции e^(x^3)*x^2 чтобы использовать фундаментальную теорему исчисления.

$\int{e^{x^{3} }x^2 } \, dx$ .

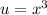Пусть u=x^3 , тогда $x=\sqrt[3]{u}$ .

$du = 3x^2dx \\ dx = \frac{du}{3x^2} = \frac{du}{3(\sqrt[3]{u} )^{2}} = \frac{du}{3u^{2/3}}$

Делаем подстановку в наше изначальное выражение:

$\int{e^{x^{3}}x^2dx}=\int{e^{u}(\sqrt[3]{u})^{2}\frac{du}{3u^{2/3}} } = \int{ e^uu^{2/3}\frac{du}{3u^{2/3}} }$

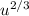Здесь $u^{2/3}$ сокращаются и мы имеем 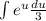$\int{e^u\frac{du}{3}}$ . Выносим 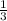$\frac{1}{3}$ за интеграл: 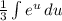$\frac{1}{3} \int{e^u} \, du$ . Теперь мы имеем знакомый интеграл, который равняется 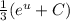$\frac{1}{3} (e^{u}+C)$ , тоже самое что 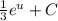$\frac{1}{3} e^u+C$ . Подставляем 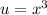u=x^3 и имеем 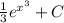$\frac{1}{3}e^{x^3}+C$ . Используем фундаментальную теорему исчисления:

$\int\limits^1_0 {e^{x^3} x^2} = \frac{1}{3} e^{x^3}]_0^1=\frac{1}{3} e^{1^3}-\frac{1}{3} e^{0^3}=\frac{1}{3} e^1-\frac{1}{3} e^0=\frac{1}{3} e-\frac{1}{3}=\frac{e-1}{3}$