2. На рисунке 15 изображено дерево некоторого случайного опыта с началом в точке ѕ. События А и В изображены промежуточными вершинам дерева. Сколько элементарных событий этого опыта благоприятствуют: а) событию А: б) событию В?
Воспользуемся методом, позволяющим находить в разложении многочлена на скобки выражения вида Если a>0, это сразу дает два решения если a<0, действительные корни эта скобка не дает, но по любому степень многочлена будет понижена на 2. Кстати, решения вида я называю парными; название мне кажется оправданным. Легко доказать, что многочлен P(x) имеет парные корни тогда и только тогда, когда они обращают в ноль по отдельности сумму четных степеней и сумму нечетных степеней. Это следует из того, что сумма четных степеней равна а сумма нечетных равна
Кстати, это утверждение будет работать и для нулевого корня, если считать, что ноль является парным корнем, в том случае, когда он является кратным.
1) Разбиваем на четные и нечетные степени:
найденные t удовлетворяют и первому уравнению, поэтому оно принимает вид (t-2)(t+1)(t+3)=0, а поскольку исходное уравнение может быть получено в виде суммы этих двух, получаем
Воспользуемся методом, позволяющим находить в разложении многочлена на скобки выражения вида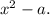
Если a>0, это сразу дает два решения 
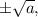если a<0, действительные корни эта скобка не дает, но по любому степень многочлена будет понижена на 2. Кстати, решения вида 
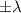я называю парными; название мне кажется оправданным. Легко доказать, что многочлен P(x) имеет парные корни 
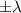тогда и только тогда, когда они обращают в ноль по отдельности сумму четных степеней и сумму нечетных степеней. Это следует из того, что сумма четных степеней равна 
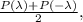а сумма нечетных равна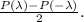 
Кстати, это утверждение будет работать и для нулевого корня, если считать, что ноль является парным корнем, в том случае, когда он является кратным.
1) Разбиваем на четные и нечетные степени: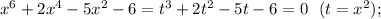
найденные t удовлетворяют и первому уравнению, поэтому оно принимает вид (t-2)(t+1)(t+3)=0, а поскольку исходное уравнение может быть получено в виде суммы этих двух, получаем
(t-2)(t+1)(t+3)-2x(t-2)(t+1)=0; (t-2)(t+1)(t-2x+3)=0; (x²-2)(x²+1)(x²-2x+3)=0.
ответ:
2) t³+6t²+11t+6=0; -2x(t^2+3t+2)=-2x(t+1)(t+2)=0;
t³+6t²+11t+6=(t+1)(t+2)(t+3); все уравнение принимает вид
(t+1)(t+2)(t+3)-2x(t+1)(t+2)=(t+1)(t+2)(t-2x+3)=(x²+1)(x²+2)(x²-2x+3)=0.
ответ: решений нет.
Пошаговое объяснение:
1)Розкладемо на прості множники 12 и 18
12 = 2 * 2 * 3
18 = 2 * 3 * 3
НСД (12 и 18) = 2 * 3 = 6
НСК (12 и 18) = 2 * 2 * 3 * 3 = 36
2) Розкладемо на прості множники 35 і 88
35 = 5 *7
88 = 2*2 *2* 11
НСД (35; 88) = 1
НСК (35, 88) = 2 *2 *2 *11 * 5 *7 = 3080
3) Розкладемо на прості множники 72; 96 і 120
72=2*2*2*3*3
96=2*2*2*2*2*3
120=2*2*2*3*5
НСД ( 72, 96,120) = 2*2*2*3= 24
НСК (72, 96, 120) = 2*2*2*2*2*3*3*5 = 1440
2) Для того, щоб знайти скільки учнів у класі, знайдемо найбільший спільний дільник 58 і 87
Разкладемо на прості множники 58 і 87
58 = 2* 29
87 = 3 *29
НСД (58; 87) = 29 = 29 всього учнів у класі