2.Сколькими можно расставить цифры от 0 до 9 вместо ∗ в выражении 2025∗∗∗∗ таким образом, чтобы полученное число делилось на 5, 6 и 2?
ответ:
а, -ов).
3.В каждой клетке шахматной доски размера 64×64 записано число, равное количеству клеток, в которые может попасть шахматный конь, если бы он стоял на данной клетке. Чему равна сумма чисел, написанных на доске?
ответ:
4.Сколько существует натуральных x, y, z, удовлетворяющих уравнению НОК(x;y;z)=735?
(В ответе запиши только число!)
ответ:
5.Реши в целых неотрицательных числах уравнение:
x1+1x2+1x3+1x4=116.
( начисляются только за полностью верное решение!)
ответ: x1=
;x2=
;x3=
;x4=
6.Каждую грань правильной пирамиды SA1A2...A4 с основанием A1A2...A4 разрешается раскрасить в один из 11 цветов. Сколькими можно раскрасить пирамиду при условии, что все грани будут разного цвета? Раскраски считаются различными, если не получаются друг из друга вращением пирамиды.
ответ:
а, -ов).
7.Найди наименьшее возможное значение функции
F(x,y)=3x2+4xy+3y2−2x+2y+10,
если числа x, y пробегают всевозможные действительные числа.
ответ:
9.Сколько существует натуральных чисел, не превосходящих 500, для которых после умножения на 1296 количество делителей увеличивается в 5 раз? (Укажи в ответе только число!)
ответ:
10.Найди сумму натуральных чисел, не превосходящих 2100, которые делятся на 2 и 3, но не делятся на 7.
ответ:
11.азовём высотой натурального числа N наибольшее возможное n, при котором уравнение
N=x1x2...xn
разрешимо в целых числах xi≥2. Сколько существует чисел максимальной высоты, не превосходящих 1015?
ответ: существует
чисел.
12.Реши следующие уравнения в натуральных числах n и k:
а) 1!+...+n!=(1!+...+k!)2;
б) 1!+...+n!=(1!+...+k!)4, где n!=1⋅2⋅...⋅n.
ответ:
а) n=
,k=
;n=
,k=
;
б) n=
,k=
Пошаговое объяснение:
Задача №1.
Я, если честно, не понимаю формулировку "запиши ответ между корнями".
Но зато я попробую тебе решить данное уравнение.
Воспользуемся дискриминантом.
Вот формула:
x1,2 = ±b ± /2а
/2а
Где: b - второй коэффициент(который мы берем с противоположным знаком); а - это первый коэффициент(он же старший коэффициент); с - свободный член.
Подставим данные:
x1,2 = 7 ±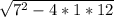 /2*1 = 7 ±1/2
/2*1 = 7 ±1/2
Тогда:
x1 = 4
x2 = 3
Задача №2
Ну для начала 7 умножим на 2 и получим 14.
Тогда имеем:
2^2 - 14 + 12.
От нас требуется извлечь корень из этого выражения.
Задача №3.
2 в квадрате = 4
Получили:
x^2 - 7x + 12 = 4
Переносим все вправо с изменением знака на противоположный.
x^2 - 7x + 8 = 0
Используя дискриминант, получаем следующие корни:
x1 =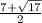
x2 = 7 - корень из 17 поделить на 2
Ким бути? Це питання стоїть перед кожним випускником, який сьогодні закінчує школу.
Мені б хотілося бути юристом. Свідомий це крок чи ні? Так, свідомий. І передусім він пов'язаний із бажанням робити людям добро, захищати їх, оберігати їхній спокій. Це є честю і гідністю кожного чоловіка. Хоч лицарство давно в минулому, але справжні чоловіки не перевелися. Я знаю багато своїх однолітків, які сильні, загартовані, міцні і дужі. Вони готові до життя.
Яке воно буде? Спокійне чи бурхливе, щасливе, чи нещасне? Це залежить від багатьох обставин і людей. Але я знаю, що це залежить і від правоохоронних органів. Стояти на боці закону, людей, допомагати їм, чи це не є мрією багатьох юнаків?
Поспішати робити добро... В цьому, мабуть, щастя людини.
Професія юриста — одна з найпочесніших на землі. Стати юристом, правоохоронцем легко, а от бути їм значно важче. Ця професія вимагає від людини знань, умінь, мужності, сили волі. І навіть за наявності всіх цих рис найважливішою має бути людяність. Треба завжди залишатися людиною.
Професіоналізм і людяність — це дві головні ознаки моєї майбутньої професії.