2) Сторона квадрата равна 16 см. Найдите площадь второго квад- 1 рата, если его периметр составляет от периметра первого 32 квадрата. напишите как задача (с краткой записью)
Родиться мужчиною мне повезло, Быть сильным и стойким, всем бедам назло! Пока что я в школе простой ученик, Но двойками мой не испорчен дневник. Учиться прилежно совсем не ленюсь, И к знаниям новым охотно стремлюсь. Люблю я компьютер, футбол и борьбу, - Со спортом свою подружил я судьбу. Пускай прозвучит это несколько грубо, Но жизнь – это клёво, и жизнь – это круто! А будут проблемы к нам – К простым и отзывчивым богатырям! Сильный и ловкий, Водит машину. Кто я такой? Настоящий мужчина! Ну и для самых умных юных всезнаек: Знаю я всё на уроках, На вопросы отвечаю, Понимаю всё на свете, И науку уважаю!
Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на , получаем
В левой части уравнения это ни что иное как формула производной частного, то есть :
Подсчитаем отдельный интеграл по частям.
2)
Это линейное однородное дифференциальное с постоянными коэффициентами. Замена , перейдём к характеристическому уравнению: , корни которого и . Тогда общее решение диф. уравнения: и его первая производная .
Осталось найти константы C₁ и C₂ , подставляя начальные условия.
Быть сильным и стойким, всем бедам назло!
Пока что я в школе простой ученик,
Но двойками мой не испорчен дневник.
Учиться прилежно совсем не ленюсь,
И к знаниям новым охотно стремлюсь.
Люблю я компьютер, футбол и борьбу, -
Со спортом свою подружил я судьбу.
Пускай прозвучит это несколько грубо,
Но жизнь – это клёво, и жизнь – это круто!
А будут проблемы к нам –
К простым и отзывчивым богатырям!
Сильный и ловкий, Водит машину. Кто я такой? Настоящий мужчина! Ну и для самых умных юных всезнаек: Знаю я всё на уроках, На вопросы отвечаю, Понимаю всё на свете, И науку уважаю!
1)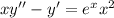
Поскольку x = 0 не является решением данного дифференциального уравнения, то поделим обе части уравнения на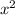 , получаем
, получаем
В левой части уравнения это ни что иное как формула производной частного, то есть :
Подсчитаем отдельный интеграл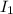 по частям.
по частям.
2)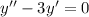
Это линейное однородное дифференциальное с постоянными коэффициентами. Замена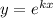 , перейдём к характеристическому уравнению:
, перейдём к характеристическому уравнению: 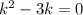 ,
, 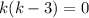 корни которого
корни которого 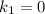 и
и 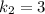 . Тогда общее решение диф. уравнения:
. Тогда общее решение диф. уравнения: 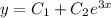 и его первая производная
и его первая производная 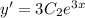 .
.
Осталось найти константы C₁ и C₂ , подставляя начальные условия.