20. Өрнектердегі жай бөлшектерді ондық бөлшекке айналдырып алып, 21. Өрнектердегі ондық бөлшектерді жай бөлшекке айналдырып алып,
есептеңдер:
1) 2 1,83;
5
3
2) 6, 4 -
20
3
3) 9, 8.
10
1
4) 7, 2:
100"
есептеңдер:
1
1) 8,5-2;
2) - 1,8;
3) 50,
0, 12;
3
Menyant
4) 0,6.
ответ: D=77 кг, а Е=47 кг, то С=329-(77+47)=205 кг
В=248 кг, то F =433-248=185 кг
G=108 кг, то А=271-108=163 кг
А=163 кг
В=248 кг
С=205 кг
D=77 кг
Е=47 кг
F =185 кг
G=108 кг
Если лифт не может поднять больше 475 кг и алфавитный порядок не может быть нарушен, то
Первый рейс - А и В едут вместе (163+248=411<475) C к ним не поместиться (411+205=616>475)
Второй рейс - C, D, E едут вместе (205+77+47=329<475) F к ним не поместиться (329+185=514>475)
Поэтому F и G едут вместе третьим рейсом - 185+108=293<475
Сответственно, наименьшее возможное количество поездок = 3
Пошаговое объяснение:
1) 3 целых 2)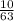 3) 8
3) 8 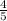
Пошаговое объяснение:
смотри 1)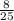 умножить на 15 +
умножить на 15 + 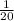 умножить на 4 умножить на
умножить на 4 умножить на 
представляем что 15 это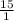 после чего умножаем
после чего умножаем 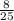 на
на 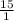 8 умножить на 15 = 120, а 25 на 1 = 25 получаем дробь
8 умножить на 15 = 120, а 25 на 1 = 25 получаем дробь 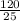 Оставляем, после умножаем
Оставляем, после умножаем 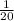
на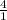 получаем
получаем 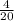 После
После 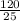 +
+ 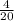 находим общий множитель это у нас 100
находим общий множитель это у нас 100
, умножаем каждое число на столько раз чтобы в множителе получилось 100 вот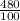 +
+ 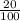 =
= 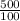 = 5 целых умножаем на
= 5 целых умножаем на  представляем
представляем 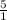 умножить на
умножить на  =
= 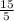 = 3 целых
= 3 целых
2-ое решаем также
скобки вычисляем сперва будет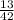 умножить на
умножить на 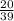 =
= 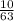 (уже сокращено)
(уже сокращено)
и 3-е аналогично
скобки потом умножение потом сумма = итог получается таков: