23. :
Н
19.
Товар
Булочка
Пирожа
Пряник
1) Начерти в тетради окружность. Выскажи
предположение о том, на сколько частей раз-
делят эту окружность три отмеченные на ней
точки.
Проверь себя: Отметь на окружности три точ-
ки и посчитай, на сколько частей разделилась
окружность.
Как ты думаешь, на сколько частей разделят
окружность четыре отмеченные на ней точки?
Выполни проверку.
2) Начерти в тетради отрезок. Сколько точек
понадобится, чтобы разделить отрезок: на три
части; на четыре части?
Сравни решение этих задач. Е лено
Сырок
24. .
20.
Начерти на клетчатом листе бумаги квадрат

Показать ответ

Ответ:

Ульяна2732

09.01.2023 09:51

№ 15 80 м²; № 16 а) 32см; b) 30° и 150°; с) 30 см²

Пошаговое объяснение:

№15

Дано: АВСD - параллелограмм

DЕ ⊥ВC; DЕ = 8м; DK⊥AC; DK = 5м

∠САD = 30°

Найти: S( АВСD)

Решение

Рассмотрим Δ АКD DК⊥AC -по условию. ⇒Δ АКD - прямоугольный, DК -катет, АD - гипотенуза. ∠CAD =30° -- по условию ⇒ DК равен половине гипотенузы АD, ⇒АD = 2DК = 2 * 5 = 10 м

Так как АВСD - параллелограмм по условию, то его противоположные стороны равны, т.е ВС = АD = 10 м. И DЕ по условию является высотой, проведенной к стороне ВС

S(АВСD) = ВC * DЕ = 10 * 8 = 80 м²

ответ: 80 м²

№ 16

В параллелограмме АВСD биссектриса ∠ D пересекает сторону ВС в точке К. Если ∠ ВКD = 105°, ВК = 4 см, КС = 6 см, то найдите:

а) периметр

b) углы

с) площадь параллелограмма

Решение

Так как противоположные стороны параллелограмма параллельны, то углы ∠ВКD и ∠ADК являются односторонними при ВС║AD и секущей КD , ⇒ ∠ВКD + ∠ADК = 180° , ⇒ ∠ADК = 180° - 105° = 75°

Т.к. КD биссектриса по условию, то ∠ADК = ∠КDС = 75°, а ∠АDС = 2*75° = 150°.

Рассмотрим Δ КDC Он - равнобедренный, так как ∠ADК = ∠КDС являются углами при его основании КD, ⇒ равенство боковых сторон КС = DС = 6 см. Так как сумма углов тр-ка равна 180°, то ∠КСD = 180° - 75° -75° = 30°

Опустим от вершины А параллелограмма АВСD высоту АЕ на продолжение стороны СD . В полученном Δ АDЕ ∠АDЕ = 180° - ∠АDС = 180° - 150° = 30° ( так как эти углы смежные)

В Δ АDЕ по построению АЕ является катетом. Так как он лежит против угла в 30°, то будет равен половине гипотенузы АD. АD = ВС -- как противоположные стороны параллелограмма. ВС= ВК + КС = 4 + 6 = 10 см; ⇒ АD = 10 см; АЕ = 1/2 АD = 10/2 = 5 см

а)Р(АВСD) = 2*ВС + 2*DС = 2*10 +2*6 = 32 см

б) противоположные углы параллелограмма равны

∠А = ∠С = 30°

∠В = ∠D = 150°

в) S(АВСD) = АЕ * DС = 5 * 6 = 30 см²

ответ: а) 32 см; b) 30° и 150°; с) 30 см²

0,0(0 оценок)

Ответ:

Натали2004абвг

12.12.2022 15:14

Задача. На сторонах АВ, ВС, СА треугольника АВС выбраны точки Р, Q и R соответственно так, что ВQ = ВР и АР = AR. Оказалось, PQ биссектриса угла ВQR. Hайдите угол ARP, eсли угол QRC равен 69°. ответ дайте в градусах.

Пусть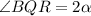 $\angle BQR=2\alpha$ , тогда поскольку PQ - биссектриса, то 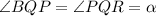$\angle BQP=\angle PQR=\alpha$ , но по условию, PB = BQ ⇒ ΔBPQ - равнобедренный, следовательно, 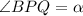$\angle BPQ=\alpha$ , но так как 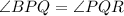$\angle BPQ=\angle PQR$ - накрест лежащие углы равны, то 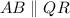$AB \parallel QR$ (первый признак параллельности прямых).

$\angle CRQ=\angle CAB$ как соответственные углы при AB || QR и секущей CA.

Аналогично, по условию AP = AR ⇒ ΔAPR - равнобедренный, следовательно,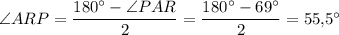 $\angle ARP=\dfrac{180^\circ-\angle PAR}{2}=\dfrac{180^\circ-69^\circ}{2}=55{,}5^\circ$