Словами описываем формулу: из первой партии И годная ИЛИ из второй партии И годная.
Дополнительно из таблицы можно найти, что вероятность брака 0,20, а в сумме (по формуле Байеса) вероятность ГОДНОЙ детали можно сказать одинаковая (0,53 : 0,47) а вот вероятность брака разная (3 : 5).
1)
Проверим точку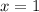 . Равенство не выполняется.
. Равенство не выполняется.
Значит, домножим и поделим на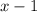 .
.
Получим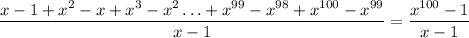 .
.
Имеем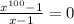 .
.
Выражение в числителе над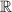 эквивалентно
эквивалентно 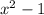 , т.к. имеет те же корни
, т.к. имеет те же корни ![x^{100} = 1 \Rightarrow x = \sqrt[100]{1} = \pm 1](/tpl/images/0977/3396/ad536.png) .
.
Значит, единственный корень: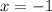 .
.
2)
При данных ограничениях решить уравнение невозможно. Сумма слева может расходиться (т.е равняться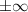 ), ведь знаменатель прогрессии
), ведь знаменатель прогрессии 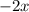 .
.
Пусть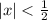
Слева имеем сумму бесконечно убывающей геометрической прогрессии. Значит выражение можно свернуть в:
Или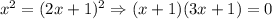 .
.
По условию подходит один корень: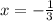
3)
Для простоты преобразуем к виду:
Слева сумма бесконечно убывающей геометрической прогрессии.
И корни:
ответ: Вероятность стандартной - 0,8.
Пошаговое объяснение:
Решение задачи сведено в таблицу. Таблица в приложении.
Задача своидтся к двум событиям: Р1 - взять случайную деталь, Р2 - взять годную, стандартную.
Следует понимать что партии деталей одинакового размера и вероятности Р1 = Р2 = 0,5.
Вероятность брака Р2 - дана, но нам нужна вероятность годной детали - по формуле q21 = 1 - p21 = 1 - 0.15 = 0.85 и q22 = 0.75.
Главное в задаче: вероятность события состоит из двух: они описываются как "И" из первой партии "И" годная "ИЛИ" из второй "И" годная.
Запоминаем на всю жизнь:
1. Вероятность события "И" равна произведению вероятностей каждого.
2. Вероятность события "ИЛИ" равна сумме вероятностей каждого.
Записываем формулу "нашего" события:
Q(A) = p1*q1 + p2*q2 = 0.5*0.85 + 0.5*0.75 = 0.425+0.375 = 0.80 - ОТВЕТ.
Словами описываем формулу: из первой партии И годная ИЛИ из второй партии И годная.
Дополнительно из таблицы можно найти, что вероятность брака 0,20, а в сумме (по формуле Байеса) вероятность ГОДНОЙ детали можно сказать одинаковая (0,53 : 0,47) а вот вероятность брака разная (3 : 5).