номер обязательно возрастает, увеличивается на 1, 1, 2, 3 и т д
года НЕвозрастают, то есть или такой же как и был или увеличивается на 1
но года не могут перепрыгнуть (повторяться могу а перепрыгнуть не могут)
и года в среднем растут медленнее чем номера
все
это возрастающие последовательности, непрерывные с точки зрения того, что все натуральные числа обязательно попадутся для номеров с1 а для годов с 2001
номера растут быстрее значит они догонят года и где-то продублируются так как числа пропускаться не могут
Среди этих чисел не может быть числа, оканчивающегося на 0, так как на 0 не делится никакое число.
Значит, эти числа либо от до , либо от до .
Значит, в любом случае среди этих чисел есть следующие:
, делящееся на 2
, делящееся на 3
, делящееся на 4
, делящееся на 5
, делящееся на 6
, делящееся на 7
, делящееся на 8
Рассмотрим утверждение "" делится на 4"". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит делится на 4, делится на 4, делится на 4, делится на 2, значит - четное.
Рассмотрим утверждение "" делится на 3"". Число делится на 3, если сумма цифр числа делится на 3. Значит, делится на 3, делится на 3. Выпишем пары цифр, где , а - четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
Рассмотрим утверждение "" делится на 7"". Если делится на 7, то делится на 7, делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
Мы учили делимость на 3, 4 и 7. Делимость на 2, 5 и 6 будет выполняться автоматически. Проверим делимость на 8. Число 428 не делится на 8, а число 848 делится на 8.
Число 841, очевидно, делится на 1, а число 849 не делится на 9. Значит, это числа от 841 до 848, а сумма цифр наименьшего числа равна 8+4+1=13.
номер обязательно возрастает, увеличивается на 1, 1, 2, 3 и т д
года НЕвозрастают, то есть или такой же как и был или увеличивается на 1
но года не могут перепрыгнуть (повторяться могу а перепрыгнуть не могут)
и года в среднем растут медленнее чем номера
все
это возрастающие последовательности, непрерывные с точки зрения того, что все натуральные числа обязательно попадутся для номеров с1 а для годов с 2001
номера растут быстрее значит они догонят года и где-то продублируются так как числа пропускаться не могут
Среди этих чисел не может быть числа, оканчивающегося на 0, так как на 0 не делится никакое число.
Значит, эти числа либо от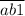 до
до 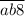 , либо от
, либо от 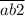 до
до 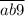 .
.
Значит, в любом случае среди этих чисел есть следующие:
Рассмотрим утверждение ""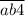 делится на 4"". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит
делится на 4"". Число делится на 4, если число, образованное двумя последними цифрами делится на 4. Значит 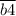 делится на 4,
делится на 4, 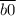 делится на 4,
делится на 4, 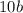 делится на 4,
делится на 4, 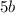 делится на 2, значит
делится на 2, значит 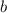 - четное.
- четное.
Рассмотрим утверждение ""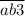 делится на 3"". Число делится на 3, если сумма цифр числа делится на 3. Значит,
делится на 3"". Число делится на 3, если сумма цифр числа делится на 3. Значит, 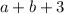 делится на 3,
делится на 3, 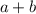 делится на 3. Выпишем пары цифр, где
делится на 3. Выпишем пары цифр, где 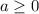 , а
, а 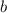 - четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
- четное, в сумме кратные 3: (1; 2); (1; 8); (2; 4); (3; 0); (3; 6); (4; 2); (4; 8); (5; 4); (6; 0); (6; 6); (7; 2); (7; 8); (8; 4); (9; 0); (9; 6).
Рассмотрим утверждение ""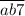 делится на 7"". Если
делится на 7"". Если 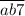 делится на 7, то
делится на 7, то 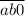 делится на 7,
делится на 7, 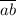 делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
делится на 7. Из ранее выписанных пар только пары (4; 2); (8; 4) удовлетворяют этому условию.
Мы учили делимость на 3, 4 и 7. Делимость на 2, 5 и 6 будет выполняться автоматически. Проверим делимость на 8. Число 428 не делится на 8, а число 848 делится на 8.
Число 841, очевидно, делится на 1, а число 849 не делится на 9. Значит, это числа от 841 до 848, а сумма цифр наименьшего числа равна 8+4+1=13.
ответ: 13