3 точки А, взятої поза площиною а, проведено до неї дві похилі. Знайдіть відстань від точки А до площини а, якщо одна з похилих на 8 см більша другої, а проекції похилих на цю площину дорівнюють 2 см і 14 см.

Центр ромба - это точка пересечения его диагоналей.

Найдем сторону a ромба (у ромба все стороны равны):

a = P/4 = 40см/4 = 10см.

Пусть диагонали ромба d₁ и d₂.

По условию d₁/d₂ = 3/4.

d₁ = 3t,

d₂ = 4t.

Диагонали ромба перпендикулярны друг другу и точкой пересечения делятся пополам. Тогда по т. Пифагора для ΔAOB имеем

a² = (d₁/2)² + (d₂/2)² = (3t/2)² + (4t/2)² = (9t²/4) + (16t²/4) = 25t²/4,

(10см)² = 100см²= 25t²/4,

t² = 100·4/25 см² = 4² см²,

см.

d₁ = 3·4 = 12 см

d₂ = 4·4 = 16 см.

Найдём расстояния от точки M до вершин ромба. По т. Пифагора для

ΔMOA имеем

AM² = MO² + (d₂/2)² = (8см)² + (16см/2)² = (64 + 64) см² = 64·2 см²

см.

По т. Пифагора для ΔMOB имеем:

MB² = MO² + (d₁/2)² = (8см)² + (12см/2)² = (64 + 36) см² = 100 см²

см.

ответ.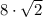 см, 10 см.

Пошаговое объяснение:

1)3-(4+3х)-14=0  розкриємо дужки , отримаємо -3х=15   х=-5

2)13*(4-х)=26       -13х=-26       х=2

3)5(0,4х-1)-0,4х=21         - 0,2х=26  х=-26/0,2=130

8)3х+2/5-4+х/3+2х-3/45=-1  зведемо до спільного знаменника, розкриємо дужки і отримаємо:14х=44     х=11

9)х/х-3+9/(х-3)(х+3)-4/х+3=1   в чисельнику будемо мати :х²-х+21/(х-3)(х+3)=1

    в знаменнику  (х-3)(х+3)≠0    х≠±3     і це квадратне рівняння не має розвязків, тому що Д∠0

(3-2х)*4+(х-2)*3-3(-х-2)≥-2         12-8х+(3х-6)+3х+6≥-2    -2х≥-14   х≥7