3 Задачи для самостоятельного решения (в классе и дома). 1). Сколькими различными могут сесть на скамейку
а) 5 человек,
б)7человек
2). Сколько различных трехцветных флагов с тремя горизонтальными полосами можно получить,
используя красный, синий и белый цвета?
3). Сколькими можно расставить по этапам четырёх участниц эстафеты в беге 4 x 100 м?
4). Составьте всевозможные трёхзначные числа, в которых все цифры разные, используя лишь цифры:
а) 7, 5, 1; 6) 2, 0. 9.
5). Сколько четырехзначных чисел можно составить из цифр 1, 2, 5, 7, если каждая цифра может
использоваться только один раз?
6). Учащиеся должны посетить во вторник по расписанию 5 уроков по следующим предметам:
литература, алгебра, география, физкультура и биология. Сколькими можно составить
расписание на этот день, чтобы физкультура была пятым уроком?
7). Из цифр 2, 3, 4, 7 составлены всевозможные четырёхзначные числа (без повторения цифр). Сколько
среди этих чисел таких, которые
а) начинаются с цифры 7:
б) не начинаются с цифры 4?
8). Из цифр 1, 2, 3, 5, 6 составлены всевозможные пятизначные числа (без повторения цифр). Сколько
среди этих чисел таких, которые:
а) кратны 4;
б) кратны 5?
9). В автомашине 5 мест. Сколькими в этой автомашине могут разместиться 5 человек, если
место водителя могут занять только двое из них?
10). Чтобы открыть сейф, нужно набрать шифр, содержащий определённую последовательность из цифр
1, 2, 3, 4, 5, 6, и другой шифр, содержащий последовательность из букв a, b, c, d, в которых буквы и
цифры не повторяются. Сколько существует комбинаций, при которых сейф НЕ открывается?
11). Сколькими можно расставить на полке четыре книги по алгебре и три по геометрии,
причём так, чтобы все книги по алгебре (в любом порядке) стояли рядом?
12). Найдите сумму всех трёхзначных чисел, которые можно составить из цифр 2, 4, 6, не повторяя цифр.
13). Число а = nl + 1, где пєN , является квадратом натурального числа. Найдите наименьшее
Значение а, если:
а) а- двузначное число;
б) а– трёхзначное число.
14). Решите уравнение:
а) х! = 5040; б) х! + (х – 1)! = 5760.
Пошаговое объяснение:
№1
1-2/9=9/9-2/9=7/9 (осталось выполнить)
№2
70/105 (Сокращаем на 5)=14/21 (Сокращаем на 7)=1/3
№3
1/7+3/4 (домножаем для общего знаменателя 28)=4/28+21/28=25/28
№4
№5
7/25*5=35/25 (сокращаем на 5)=7/5=1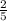 =1,4
=1,4
№6
9/28:18/35=(9*35)/(28*18) сокращаем 9 и 18 (делим на 9)=35/56=5/8
№7
5/6*х=4(1/2)
х=4(1/2)/(5/6)
х=27/5=5,4
№8
7/8*7/8=49/64
№9
5/7*35=25 (см)
№10
4(5/11)*22/98=49/11*22/98 (сокращаем (49 и 98) и (11 и 22))=2/2=1
№11
60/2*5=150
№12
Всего 68 га
Первый день 68*1/4=17 га
Второй день (68-17)*2/3=34 га
Третий день 68-17-34=17 га
№13
(7/12+11/30х):7/14=1/3
(7/12+11/30х)*14/7=1/3
22/30х=1/3-14/12
22/30х=-5/6
х=-25/22=-1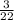
Пошаговое объяснение:
Дачи у нас расположены вдоль лесополосы.Места тихие, особо никого нет . Наша маленькая собака как обычно ушла за пределы участка и ходила по поселку. Мы знали что она и в лес тоже ходит. Однажды со стороны леса разнесся по округе громки лай , пес стояла на берегу небольшой канавки , через которую ни составляло труда просто перешагнуть, но жители которые часто ходили в лес поставили два колеса для удобства, и те в свою очередь образовали не большой туннель. Первым делом мы вышли и направились в сторону лая , мы неслись , потому что не знали, что произошло.В голове у нас представлялись жутки сцены, как собаку кто-то укусил ,а может и ещё хуже. Добравшись до места у мы увидели собаку, она рычала.скалила зубы и очень громко лаяла. Она стаяла рядом с туннелем из колес и пыталась туда забраться , но вода ей мешала. Мы заглянули и нам представилась весьма необычная картина, маленький зайчонок сидел в птичьем гнезде, оно уже разваливалось, половина ушла под воду, но тот не пытался выбраться. Мы решили протянуть руки, но потом поняли ,что он может и укусить. Нас удивляло то , почему этот заяц сидел там и даже не пытался уйти. Мы взяли мою кофту и аккуратно подняли его и тут нам стало всё ясно. На задней лапе у него была глубокая рана , мы не знали причину её появления и даже гадать не стали, но поняли зато почему заяц сидел в туннели .Мы принесли его на участок , пёс смотрела на нас с недоверием, он скорее всего не мог понять , почему же принесли это существо в дом . Мы с трудом обработали рану , так как заяц брыкался , затем попытались забинтовать, но он содрал повязку. Мы отнесли его в укромный уголок двора, где он пролежал два дня, после чего сбежал . Мы до сих пор думаем что было бы если бы наш пёс не увидел, этого раненного.
P.S. могут быть проблемы со знаками препинания. Рассказ взят из жизни