38. Дана функция f(x)=〖(4x+7)〗^(-6) . Найдите f^' (x)

7. а)15

б) Алия

с) Алия и Диана

8.                                                                        Дано:                                                                                                                             ∠AOC = 180°                                                       Найти:                                                                                                                            ∠ AOB, ∠BOC — ?

1) Пусть ∠BOC = x°. Тогда ∠AOB = x+40°. По теореме о сумме углов треугольника получаем, что x+x+40 = 180°. 

уравнение.

x+x+40 = 180

2x + 40 = 180

2x = 180-40

2x = 140 

x = 140:2

x = 70.

∠BOC = 70° ∠AOB = 70+40 = 110°

ответ: 70°, 110°.

9.а)45

P.S (не могу почему то загрузить файл )

ответ: 8 пар.

Объяснение:

Раскрыв скобки, получаем:

Перенесем слагаемые с переменными влево, а свободный член — вправо:

Из обеих частей уравнения вычтем :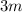

Разложим левую часть на множители методом группировки:

К обеим частям уравнения прибавим выражение :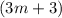

Вынесем общий множитель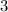 за скобки:

Вынесем :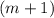

Так значения m и n целые (по нужному условию), значения выражений в скобках не могут быть дробными.

Произведение двух целых чисел равно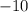 в восьми случаях:

1) ;

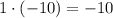2) ;

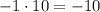3) ;

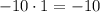4) ;

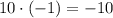5) ;

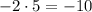6) ;

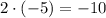7) ;

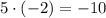8) .

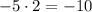Определим, какие будут значения m и n, если значения выражений в скобках равны множителям из каждого случая:

1)

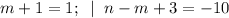
Получаем:

Значит, (m,n) = (0; -13).

Аналогично рассмотрим следующие случаи:

2)

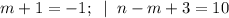
(m,n) = (-2; 5).

3)

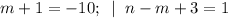
(m,n) = (-11; -13).

4)

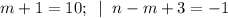
(m,n) = (9; 5).

5)

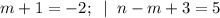
(m,n) = (-3; -1).

6)

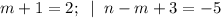
(m,n) = (1; -7).

7)

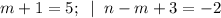
(m,n) = (4; -1).

8)

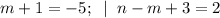
(m,n) = (-6; -7).

Выходит, 8 пар целых чисел (m, n) удовлетворяют данное равенство.