a₁ = (-3 + ) ÷ 6
a₂ = (-3 - ) ÷ 6
Пошаговое объяснение:
Решаем уравнение (3а + 1)² - (3а - 2(2 + 3а)) = 17.
По формуле сокращенного умножения (a + b)² = a² + 2ab + b² упрощаем уравнение —
9a² + 6a + 1 - (3a - 2(2 + 3a)) = 17
Далее раскрываем скобки —
9a² + 6a + 1 - (3a - 4 - 6a) = 17
9a² + 6a + 1 - 3a + 4 + 6a = 17
Теперь упрощаем и преобразовываем в квадратное уравнение —
9a² + (6a - 3а + 6а) + (1 + 4) = 17
9a² + 9a + 5 = 17
Переносим константу в левую часть равенства, меняя ее знак, и упрощаем —
9a² + 9a + 5 - 17 = 0
9a² + 9a - 12 = 0
Делим все стороны уравнения на 3 —
3a² + 3a - 4 = 0
Определяем коэффициенты квадратного уравнения a, b, с —
a = 3, b = 3, с = -4.
Подставляем полученные значения в формулу для вычисления корней квадратного уравнения х = (-b ± ) ÷ 2а —
а = (-3 ± ) ÷ (2 × 3)
Вычисляем —
а = (-3 ± ) ÷ 6
a = (-3 ± ) ÷ 6
Тогда уравнение имеет 2 корня —
a₁ = (-3 + ) ÷ 6 и a₂ = (-3 - ) ÷ 6
2.
Число скобок должно быть чётным.
Если в условии
(3а+1)² - (3а-2)(2+3а) = 17, то решение следующее:
(3а)² + 2•3а•1 + 1²) - ((3а)² - 2²) = 17
9а² + 6а + 1 - (9а² - 4) = 17
9а² + 6а + 1 - 9а² + 4 = 17
6а + 5 = 17
6а = 17 - 5
6а = 12
а = 12 : 6
а = 2
ответ: 2.
Проверка:
(3•2+1)² - (3•2-2)(2+3•2) = 17
49 - 4•78 = 17
17 = 17 - верно.
Использованы две формулы сокращённого умножения
(а+b)² = a²+2ab+b² и
(а-b)(a+b) = a²- b²
a₁ = (-3 +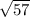 ) ÷ 6
) ÷ 6
a₂ = (-3 -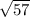 ) ÷ 6
) ÷ 6
Пошаговое объяснение:
Решаем уравнение (3а + 1)² - (3а - 2(2 + 3а)) = 17.
По формуле сокращенного умножения (a + b)² = a² + 2ab + b² упрощаем уравнение —
9a² + 6a + 1 - (3a - 2(2 + 3a)) = 17
Далее раскрываем скобки —
9a² + 6a + 1 - (3a - 4 - 6a) = 17
9a² + 6a + 1 - 3a + 4 + 6a = 17
Теперь упрощаем и преобразовываем в квадратное уравнение —
9a² + (6a - 3а + 6а) + (1 + 4) = 17
9a² + 9a + 5 = 17
Переносим константу в левую часть равенства, меняя ее знак, и упрощаем —
9a² + 9a + 5 - 17 = 0
9a² + 9a - 12 = 0
Делим все стороны уравнения на 3 —
3a² + 3a - 4 = 0
Определяем коэффициенты квадратного уравнения a, b, с —
a = 3, b = 3, с = -4.
Подставляем полученные значения в формулу для вычисления корней квадратного уравнения х = (-b ± ) ÷ 2а —
) ÷ 2а —
а = (-3 ±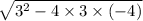 ) ÷ (2 × 3)
) ÷ (2 × 3)
Вычисляем —
а = (-3 ±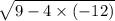 ) ÷ 6
) ÷ 6
a = (-3 ±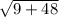 ) ÷ 6
) ÷ 6
a = (-3 ±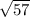 ) ÷ 6
) ÷ 6
Тогда уравнение имеет 2 корня —
a₁ = (-3 +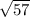 ) ÷ 6 и a₂ = (-3 -
) ÷ 6 и a₂ = (-3 - 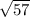 ) ÷ 6
) ÷ 6
2.
Пошаговое объяснение:
Число скобок должно быть чётным.
Если в условии
(3а+1)² - (3а-2)(2+3а) = 17, то решение следующее:
(3а)² + 2•3а•1 + 1²) - ((3а)² - 2²) = 17
9а² + 6а + 1 - (9а² - 4) = 17
9а² + 6а + 1 - 9а² + 4 = 17
6а + 5 = 17
6а = 17 - 5
6а = 12
а = 12 : 6
а = 2
ответ: 2.
Проверка:
(3•2+1)² - (3•2-2)(2+3•2) = 17
49 - 4•78 = 17
17 = 17 - верно.
Использованы две формулы сокращённого умножения
(а+b)² = a²+2ab+b² и
(а-b)(a+b) = a²- b²